d-dimensional MGL and survival MGL copula
cMGL.multi.RdDensity, distribution function, and random generation for the MGL and survival MGL copula.
dcMGL.multi(u, pars, log = FALSE)
dcMGL180.multi(u, pars, log = FALSE)
pcMGL.multi(u, pars)
pcMGL180.multi(u, pars)
rcMGL.multi(n, d, pars)
rcMGL180.multi(n, d, pars)Arguments
- u
d-dimensional matrix
- pars
copula parameter, denoted by \(\delta>0\).
- log
logical; if TRUE, probabilities/densities p are returned as log(p).
- n
number of observations. If length(n) > 1, the length is taken to be the number required.
- d
d-dimensional
Value
dcMGL.multi,pcMGL.multiandrcMGL.multigives values of Density, distribution function, and random generation for the d-dimensional MGL copula with copula parameter \(\delta>0\).dcMGL180.multi,pcMGL180.multiandrcMGL180.multigives values of Density, distribution function, and random generation for the d-dimensional MGL copula with copula parameter \(\delta>0\).
Examples
dcMGL.multi(u = cbind(c(0.6, 0.1, 0.5), c(0.3, 0.9, 0.2)), pars = 2, log = FALSE)
#> [1] 0.9331973 0.2516591 0.8466789
dcMGL.multi(u = cbind(c(0.6, 0.1), c(0.3, 0.9), c(0.5, 0.6)), pars = 2, log = TRUE)
#> [1] 0.1348624 -2.1437413
if (FALSE) {
dcMGL180.multi(u = cbind(c(0.6, 0.1, 0.5), c(0.3, 0.9, 0.2)), pars = 2, log = FALSE)
dcMGL180.multi(u = cbind(c(0.6, 0.1), c(0.3, 0.9), c(0.5, 0.6)), pars = 2, log = TRUE)
}
# 2-dim MGL copula
pcMGL.multi(u = cbind(c(0.5, 0.5), c(0.01, 0.9)), pars = 3)
#> For infinite domains Gauss integration is applied!
#> For infinite domains Gauss integration is applied!
#> [1] 0.009961138 0.478355363
# 3-dim MGL copula
pcMGL.multi(u = cbind(c(0, 0.2, 0.5), c(0.5, 0.2, 0.5), c(0.01, 0.5, 0.9)), pars = 3)
#> For infinite domains Gauss integration is applied!
#> For infinite domains Gauss integration is applied!
#> [1] 0.0000000 0.1323343 0.3524954
pcMGL180.multi(u = cbind(c(0.5, 0.5), c(0.01, 0.9)), pars = 3)
#> For infinite domains Gauss integration is applied!
#> For infinite domains Gauss integration is applied!
#> [1] 0.005363163 0.461485290
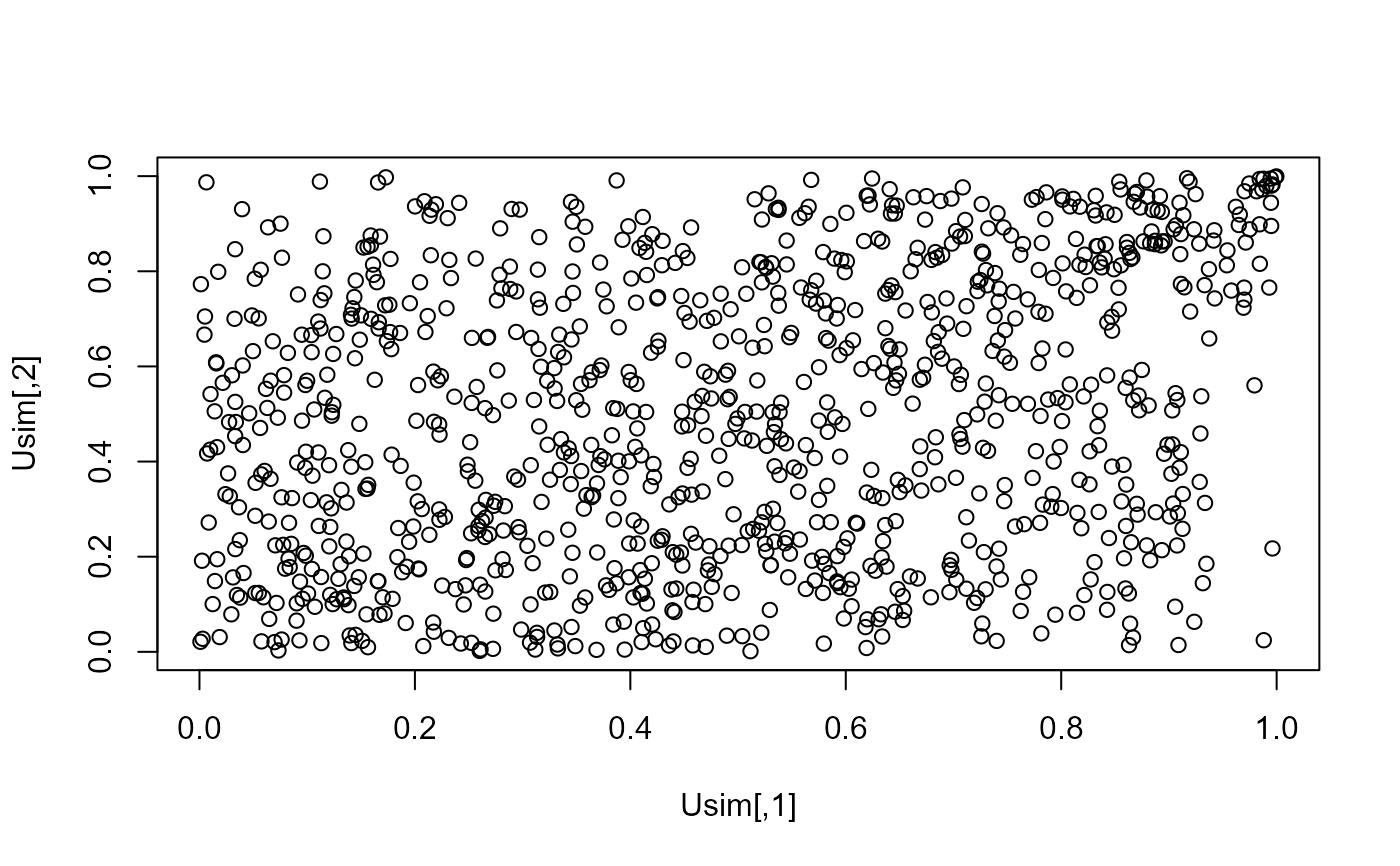
Usim <- rcMGL.multi(n = 1000, d = 2, pars = 1)
plot(Usim)
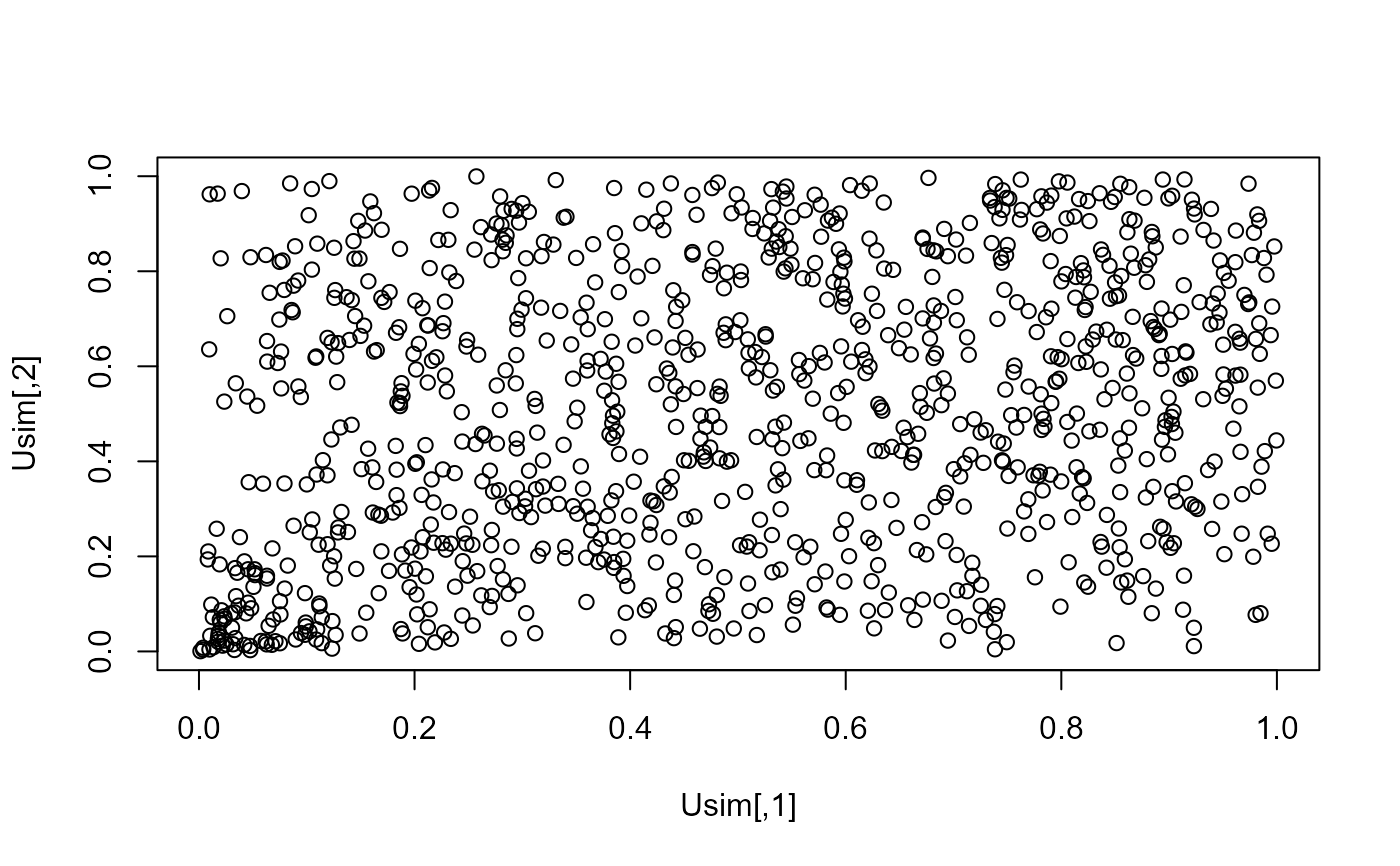 Usim <- rcMGL180.multi(n = 1000, d = 2, pars = 1)
plot(Usim)
Usim <- rcMGL180.multi(n = 1000, d = 2, pars = 1)
plot(Usim)