Simulation-study
Simluation-study.Rmd\(d=2\) without covariates
library(rMGLReg)
set.seed(112)
Usim <- rcMGL.multi(n = 1000, d = 2, pars = 2)
plot(Usim)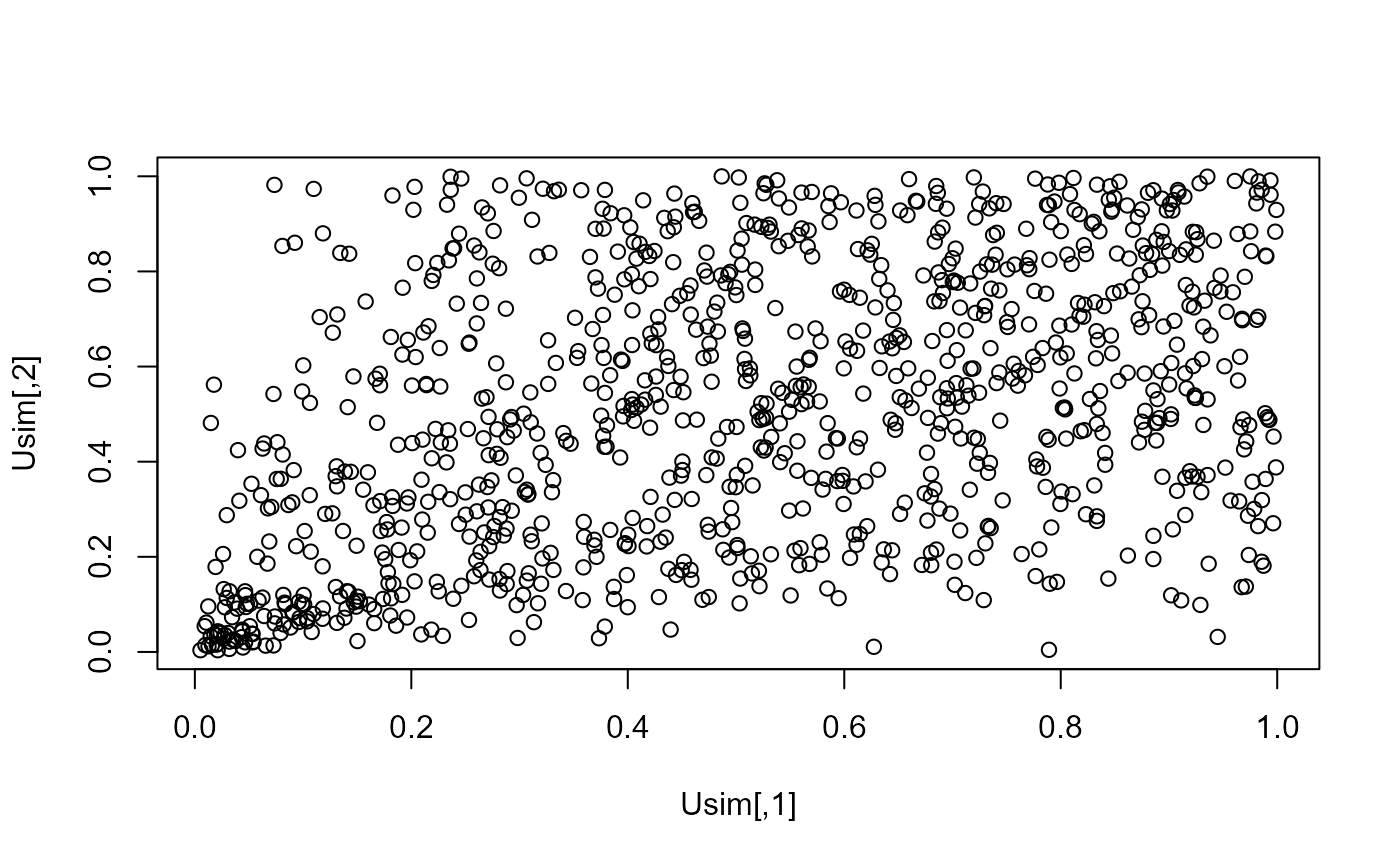
m.MGL <- MGL.mle(Usim,
copula = "MGL",
initpar = c(2), hessian = TRUE)
# estimation results
m.MGL
#> $loglike
#> [1] 178.1218
#>
#> $copula
#> $copula$name
#> [1] "MGL"
#>
#>
#> $estimates
#> [1] 1.841785
#>
#> $se
#> [1] 0.1111091
#>
#> $hessian
#> [,1]
#> [1,] -81.0029
#>
#> $AIC
#> [1] -354.2436
#>
#> $BIC
#> [1] -349.3359\(d=10\) without covariates
library(rMGLReg)
set.seed(112)
Usim <- rcMGL.multi(n = 500, d = 10, pars = 2)
round(cor(Usim, method = "kendall"), 2)
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 1.00 0.30 0.32 0.31 0.30 0.30 0.34 0.33 0.29 0.33
#> [2,] 0.30 1.00 0.27 0.26 0.27 0.27 0.28 0.31 0.29 0.25
#> [3,] 0.32 0.27 1.00 0.30 0.34 0.32 0.31 0.35 0.28 0.32
#> [4,] 0.31 0.26 0.30 1.00 0.28 0.33 0.32 0.32 0.28 0.30
#> [5,] 0.30 0.27 0.34 0.28 1.00 0.33 0.28 0.32 0.28 0.30
#> [6,] 0.30 0.27 0.32 0.33 0.33 1.00 0.29 0.33 0.29 0.33
#> [7,] 0.34 0.28 0.31 0.32 0.28 0.29 1.00 0.34 0.29 0.27
#> [8,] 0.33 0.31 0.35 0.32 0.32 0.33 0.34 1.00 0.31 0.31
#> [9,] 0.29 0.29 0.28 0.28 0.28 0.29 0.29 0.31 1.00 0.27
#> [10,] 0.33 0.25 0.32 0.30 0.30 0.33 0.27 0.31 0.27 1.00
m.MGL <- MGL.mle(Usim,
copula = "MGL",
initpar = c(2),
hessian = TRUE)
# estimation results
m.MGL
#> $loglike
#> [1] 86.09371
#>
#> $copula
#> $copula$name
#> [1] "MGL"
#>
#>
#> $estimates
#> [1] 1.896574
#>
#> $se
#> [1] 0.1617805
#>
#> $hessian
#> [,1]
#> [1,] -38.20739
#>
#> $AIC
#> [1] -170.1874
#>
#> $BIC
#> [1] -165.9728\(d=2\) with covariates \(x_1\) and \(x_2\)
# simulated the data
set.seed(111)
n <- 500
beta.true <- c(-0.6, 0.5, 0.2)
d <- 2
x1 <- rnorm(n, 0, 1)
x2 <- rnorm(n, 0, 1)
X <- model.matrix(~ x1 + x2)
delta.sim <- as.vector(exp(X%*%beta.true))
summary(delta.sim)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.06616 0.38778 0.54938 0.63676 0.76962 2.99643
Usim <- matrix(0, nrow = n, ncol = d)
for (i in 1:n){
Usim[i, ] <- rcMGL.multi(n = 1, d = d, pars = delta.sim[i])
}
plot(Usim)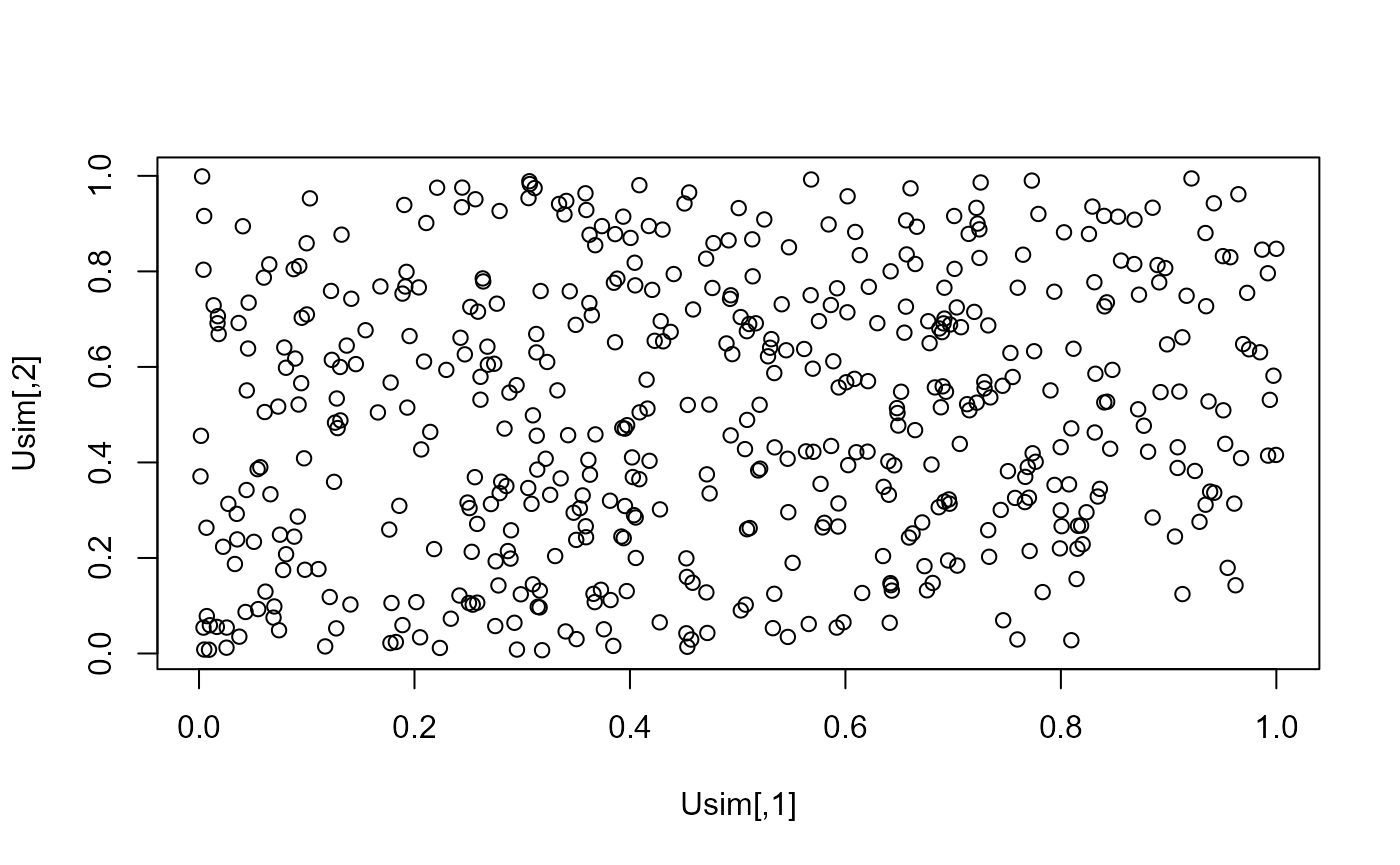
m.MGL <- MGL.reg(U = Usim,
X = X,
copula = "MGL",
hessian = TRUE,
initpar = c(-0.6, 0.5, 0.2))
# estimation results
m.MGL
#> $loglike
#> [1] 13.01003
#>
#> $copula
#> $copula$name
#> [1] "MGL"
#>
#>
#> $estimates
#> [1] -0.94374244 0.60019077 0.03849768
#>
#> $se
#> [1] 0.3071436 0.2366234 0.2538140
#>
#> $hessian
#> [,1] [,2] [,3]
#> [1,] -20.587099 -18.084391 -1.524114
#> [2,] -18.084391 -35.292517 3.768408
#> [3,] -1.524114 3.768408 -16.979663
#>
#> $AIC
#> [1] -20.02006
#>
#> $BIC
#> [1] -7.376235\(d=10\) with covariates \(x_1\) and \(x_2\)
# simulated the data
set.seed(111)
n <- 500
beta.true <- c(-0.6, 0.5, 0.2)
d <- 10
x1 <- rnorm(n, 0, 1)
x2 <- rnorm(n, 0, 1)
X <- model.matrix(~ x1 + x2)
delta.sim <- as.vector(exp(X%*%beta.true))
summary(delta.sim)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.06616 0.38778 0.54938 0.63676 0.76962 2.99643
Usim <- matrix(0, nrow = n, ncol = d)
for (i in 1:n){
Usim[i, ] <- rcMGL.multi(n = 1, d = d, pars = delta.sim[i])
}
round(cor(Usim, method = "kendall"), 2)
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 1.00 0.14 0.16 0.11 0.15 0.12 0.16 0.08 0.10 0.10
#> [2,] 0.14 1.00 0.11 0.16 0.09 0.09 0.17 0.09 0.12 0.12
#> [3,] 0.16 0.11 1.00 0.12 0.12 0.12 0.15 0.12 0.12 0.15
#> [4,] 0.11 0.16 0.12 1.00 0.18 0.12 0.16 0.13 0.08 0.16
#> [5,] 0.15 0.09 0.12 0.18 1.00 0.12 0.16 0.13 0.08 0.12
#> [6,] 0.12 0.09 0.12 0.12 0.12 1.00 0.17 0.12 0.06 0.07
#> [7,] 0.16 0.17 0.15 0.16 0.16 0.17 1.00 0.12 0.07 0.15
#> [8,] 0.08 0.09 0.12 0.13 0.13 0.12 0.12 1.00 0.08 0.11
#> [9,] 0.10 0.12 0.12 0.08 0.08 0.06 0.07 0.08 1.00 0.08
#> [10,] 0.10 0.12 0.15 0.16 0.12 0.07 0.15 0.11 0.08 1.00
m.MGL <- MGL.reg(U = Usim,
X = X,
copula = "MGL",
hessian = TRUE,
initpar = c(-0.6, 0.5, 0.2))
# estimation results
m.MGL
#> $loglike
#> [1] 453.5656
#>
#> $copula
#> $copula$name
#> [1] "MGL"
#>
#>
#> $estimates
#> [1] -0.6969649 0.5173644 0.2208068
#>
#> $se
#> [1] 0.06234517 0.04723511 0.04873398
#>
#> $hessian
#> [,1] [,2] [,3]
#> [1,] -476.3430 -365.7069 -189.7812
#> [2,] -365.7069 -731.0367 -116.1038
#> [3,] -189.7812 -116.1038 -498.6095
#>
#> $AIC
#> [1] -901.1313
#>
#> $BIC
#> [1] -888.4874