Chapter 2 风险与随机变量
学习目标:
掌握随机变量的概率/密度函数、分布函数等
掌握概率母函数/矩母函数
理解随机变量中截断和删失的原理,掌握变换后随机变量的期望计算方法
能够运用 R 语言定义分布函数等并画图
2.1 风险与随机变量
风险是指在某一特定环境下,在某一特定时间段内,某种损失发生的可能性。风险通常具有以下七个主要特征。
风险存在的客观性。风险是客观存在的,是不以人的意志为转移的。风险的客观性是保险产生和发展的自然基础。人们只能在一定的范围内改变风险形成和发展的条件,降低风险事故发生的概率,减少损失程度,而不能彻底消除风险。
风险的损失性。风险发生后必然会给人们造成某种损失,然而对于损失的发生人们却无法预料和确定。人们只能在认识和了解风险的基础上严防风险的发生和减少风险所造成的损失,损失是风险的必然结果。
风险损失发生的不确定性。风险是客观的、普遍的,但就某一具体风险损失而言其发生是不确定的,是一种随机现象。例如,火灾的发生是客观存在的风险事故,但是就某一次具体火灾的发生而言是不确定的,也是不可预知的,需要人们加强防范和提高防火意识。
风险存在的普遍性。风险在人们生产生活中无处不在、无时不有,并威胁着人类的生命和财产的安全,如地震灾害、洪水、火灾、意外事故的发生等。随着人类社会的不断前进和发展,人类将面临更多新的风险,风险事故造成的损失也可能越来越大。
风险的社会性。没有人和人类社会,就谈不上风险。风险与人类社会的利益密切相关,时刻关系着人类的生存与发展,具有社会性。随着风险的发生,人们在日常经济和生活中将遭受经济上的损失或身体上的伤害,企业将面临生产经营和财务上的损失。
风险发生的可测性。单一风险的发生虽然具有不确定性,但对总体风险而言,风险事故的发生是可测的,即运用概率论和大数法则对总体风险事故的发生是可以进行统计分析的,以研究风险的规律性。风险事故的可测性为保险费率的厘定提供了科学依据。
风险的可变性。世间万物都处于运动、变化之中,风险也是如此。风险的变化,有量的增减,有质的改变,还有旧风险的消失和新风险的产生。风险因素的变化主要是由科技进步、经济体制与结构的转变、政治与社会结构的改变等方面的变化引起的。
通常根据保险业务不同(寿险业务和非寿险业务),保险风险的具体对象有不同的含义:
寿险业务是指人身为保险标的的保险,包括长期寿险(含年金保险)业务、长期健康险业务以及长期意外险业务。其中的保险风险通常包括:
死亡、伤残等发生的风险
费用风险
退保风险
非寿险业务通常指财产险业务,通常为短期险种,主要包括保险期间为一年或一年以内的 财产保险、责任保险、短期意外险、短期健康险和短期寿险。保险风险通常包括
保费风险
准备金风险
巨灾风险
随机变量是描述不确定性的重要数学工具,因此风险可以用随机变量来表示。 随机变量是指取值依赖于随机现象的观察结果的变量,取值是随机的,取值特征通过概率分布来描述。一般用大写的英文字母表示。随机变量可以表示为:
连续型随机变量。其取值通常布满一个区间,如保险事故造成的损失金额 \(X\) 的取值范围为 \((0,+\infty)\)。
离散型随机变量。其取值为有限个或可列个值,如保险事故发生的次数 \(N\) 的取值范围为 \(0, 1, 2, 3, ...\)。保险事故是否发生损失可以表示为取值为 0 和 1 的离散型变量 \(I=0,1\)。
半连续型随机变量。其取值通常为连续型和离散型的结合,如保险事故造成的累积损失 \(S\),其取值范围为 \([0, +\infty\),其中 \(S=0\) 表示保险事故没有造成损失,\(S>0\) 表示保险事故造成了多大的损失。
| 寿险业务 | 非寿险业务 |
|---|---|
| 业务比较稳定 | 业务极其不稳定 |
| 保险金的给付具有可预期性 | 理赔频率和赔付额具有很强的随机性 |
| 保险业务具有长期性 | 业务多位短期险种 |
2.2 分布函数
连续型随机变量 \(X\) 的累积分布函数 (Cumulative Distribution Function, cdf) 表示为 \[ F_{X}(x)=\Pr(X\le x) \] 上式表明,分布函数描述了随机变量 \(X\) 小于或者等于 \(x\) 的概率。随机变量的分布函数具有下述性质:
对于任意的取值 \(x\), 都有 \(0\le F_X(x) \le 1\)
\(F_X(x)\) 是右连续型函数
\(\lim_{x\to +\infty}F_X(x)=1\)
\(\lim_{x\to -\infty}F_X(x)=0\)
【例】:运用 R 软件画出下面两种分布函数图。 \[\begin{equation*} F_1(x) = \begin{cases} 0 &\quad x <0,\\ 0.01x & \quad 0 \le x < 100,\\ 1, & \quad x\ge 100. \end{cases} \end{equation*}\]
在 R 语言中可以通过 function 函数指令来命名和创建函数。首先要给函数赋值,也就是命名,然后在小括号中写入参数,最后再大括号中写入函数要执行的语句。下面这段 R 代码定义了一个分布函数 F1.f,并使用 Vectorize() 函数将其向量化,以允许输入和输出为向量。
该分布函数 F1.f 的定义如下:
如果输入 \(x\) 小于0,则输出为0。
如果输入 \(x\) 介于0和100之间(包括0但不包括100),则输出为0.01乘以 \(x\) 的值。
如果输入 \(x\) 大于等于100,则输出为1。
在代码中,使用seq()函数生成一个从0到100的等间距序列,作为画图的横轴数据。然后,通过调用分布函数F1.f并将横轴数据作为参数,计算得到纵轴数据。最后,使用plot()函数绘制了一条连接这些数据点的蓝色曲线,并设置线宽度为2。详细代码如下:
# 定义分布函数
F1.f <- function(x) {
if (x < 0){
out <- 0
} else if(x < 100 & x >= 0){
out <- 0.01*x
} else if (x >= 100){
out <- 1
}
return(out)
}
F1.f <- Vectorize(F1.f) # 将函数向量化,允许函数输入向量,输出向量
x <- seq(from = 0, to = 100, length.out = 20) # 画图横轴数据
y <- F1.f(x) # 画图纵轴数据
plot(x, y, type = 'l', col = "blue", lwd = 2)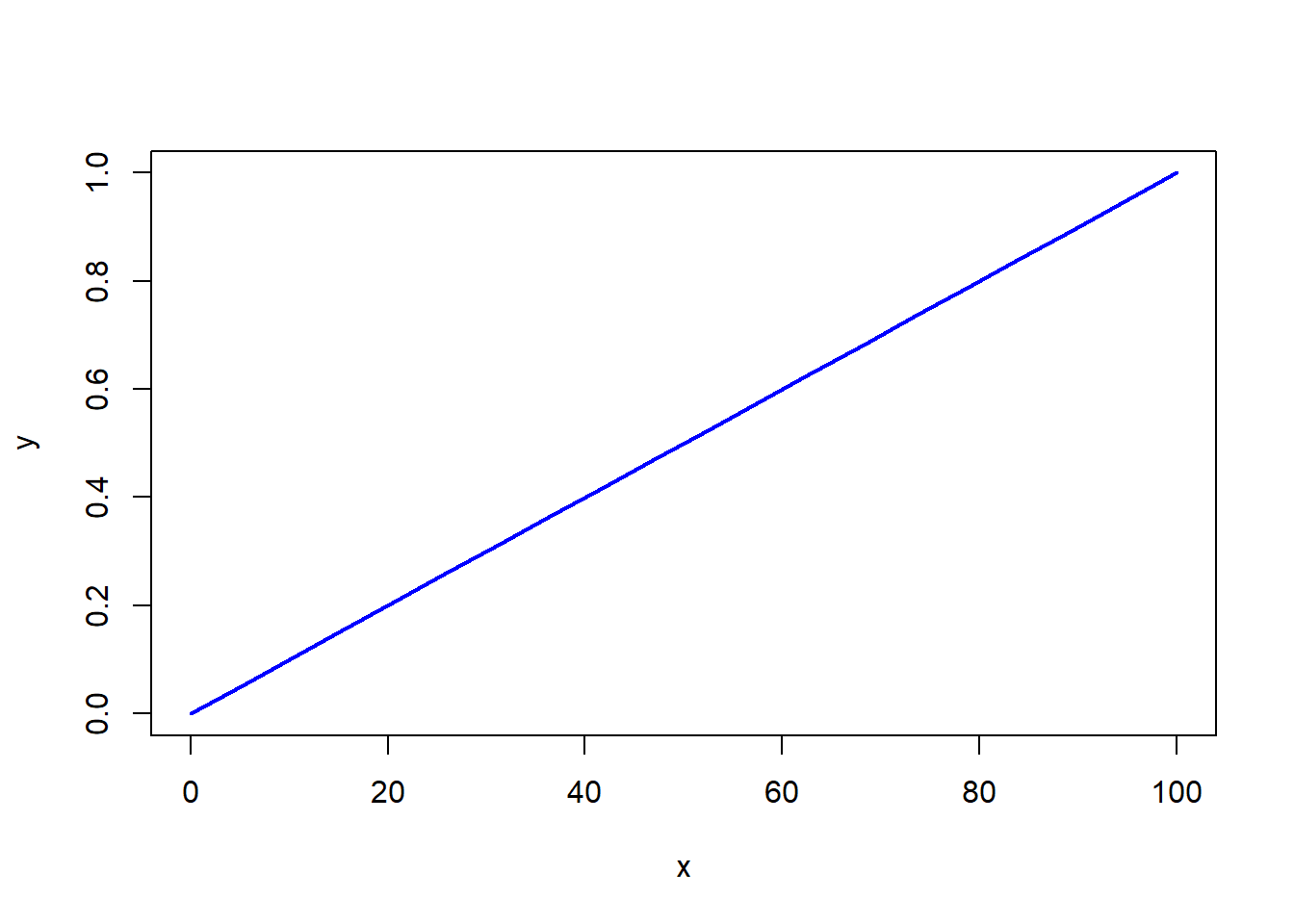
Figure 2.1: \(F_1(x)\) 的分布函数图
\[\begin{equation} F_2(x) = \begin{cases} 0 &\quad x <0,\\ 1 - \left(\frac{2000}{x + 2000}\right)^3, & \quad x\ge 0, \end{cases} \end{equation}\]
F2.f <- function(x) {
if (x < 0){
out <- 0
} else if (x >= 0){
out <- 1 - (2000/(2000 + x))^3
}
return(out)
}
F2.f <- Vectorize(F2.f)
x <- seq(from = 0, to = 3000, length.out = 100)
y <- F2.f(x)
plot(x, y, type = 'l', col = "blue", lwd = 2)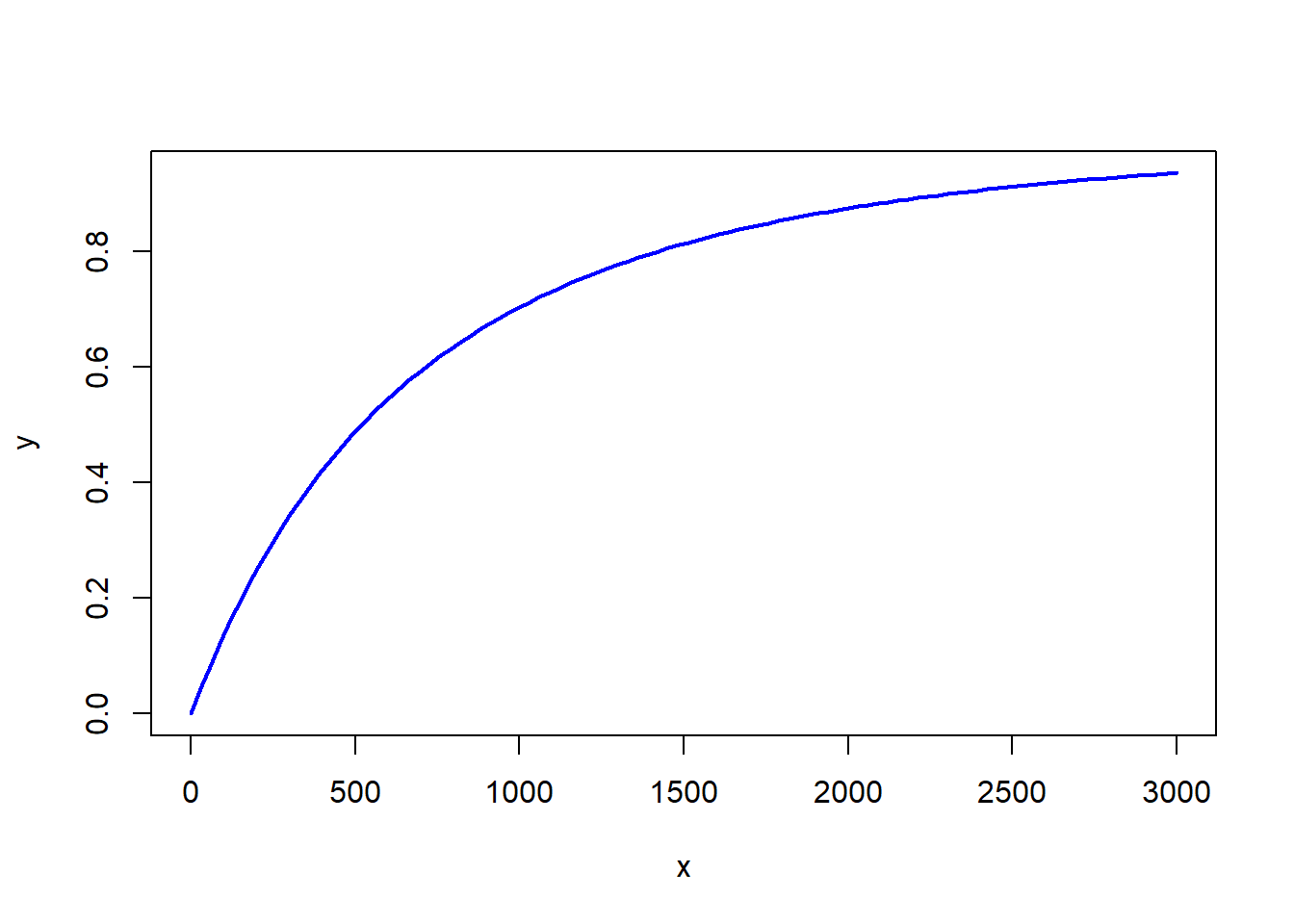
Figure 2.2: \(F_2(x)\) 的分布函数图
2.3 密度函数
保险损失通常是非负的。对于非负的连续型随机变量 \(X\), 假设其分布函数为 \(F_{X}(x)\),如果存在非负的可积函数 \(f_X(x)\),是的对于任意实数 \(x\) 有 \[ F_{X}(x)=\int_{0}^{x}f(t)dt \] 则称 \(f_X(x)\) 为随机变量 \(X\) 的密度函数。非负随机变量的密度函数具有下述性质:
2.4 生存函数
随机变量的生存函数 (Survival Function) 定义为: \[ S_{X}(x)=\Pr(X>x)=1-F_{X}(x) \] 其中,生存函数表示随机变量 \(X\) 大于 \(x\) 的概率。若随机变量是连续的,其密度函数和生存函数存在下述关系:
\[\begin{align*} S_{X}(x)&=\int_{0}^\infty f_{X}(x)dx,\\ f(x)&=-\frac{dS(x)}{dx}. \end{align*}\]
【例】:运用 R 软件画出 F2.f 对应的密度函数图。
f2.f <- function(x){
if (x > 0){
out <- 3*(2000)^3/(x + 2000)^4
} else out <- 0
return(out)
}
f2.f <- Vectorize(f2.f)
x <- seq(from = 0.001, to = 3000, length.out = 100)
y <- f2.f(x)
plot(x, y, type = 'l', col = "blue", lwd = 2)
Figure 2.3: \(S_2(x)\) 生存函数图
2.5 中心距和原点矩
如果密度函数、分布函数或生存函数是已知的,分布就会给我们提供随机变量的全部信息。如果我们不能得到分布函数的精确表达式,应该怎么办?下面我们将介绍两种刻画随机变量部分信息的指标:中心距和原点矩。
原点矩和中心距是为了提炼出一个特征数来作为代表,用于描述随机变量全部取值存在的具体情况,使得用少量的特征数来充分概括某个随机变量的全部取值。
和均值是一样的用意,均值就是用于描述随机变量全部取值的一个特征数。
【定义】假设 \(X\) 为随机变量,\(k\) 为正整数,则 \(\mathbb{E}(X^k)\) 为随机变量的 \(k\) 阶原点矩,记为 \(\mu_k'\)。 显而易见:一阶原点矩就是随机变量全部取值的期望,记为 \(\mu=\mathbb{E}(X)\)。
连续型原点距: \[ \mu_{k}'=\mathbb{E}(X^k)=\int_{-\infty}^{\infty}x^kf(x)dx. \]
离散型原点矩:
\[ \mu_{k}'=\mathbb{E}(X^k)=\sum_{j}x_j^k p(x_j). \] 其中,\(p(x_j)\) 表示随机变量在 \(x_j\) 点取值的概率。
【定义】假设 \(X\) 为随机变量,\(k\) 为正整数,则 \(\mathbb{E}[(X-\mu)^k]\) 为随机变量的 \(k\) 阶中矩,记为 \(\mu_k\)。 显而易见:一阶中心矩等于 0,二阶中心矩就是随机变量的方差。
注意:在统计与精算中常用的低阶矩,高于 4 阶的极少使用。
连续型中心距: \[ \mu_{k}=\mathbb{E}[(X-\mu)^k]=\int_{-\infty}^{\infty}(x-\mu)^kf(x)dx. \]
离散型中心矩:
\[ \mu_{k}=\mathbb{E}[(X-\mu)^k]=\sum_{j}(x_j-\mu)^k p(x_j). \]
常用的中心距和原点矩:
二阶中心距通常表示为随机变量的方差,记为 \(\sigma^2\) 或者 \(\text{Var}(X)\)。\(\sigma\) 可以表示随机变量的标准差。
标准差和均值(期望)的比值为变异系数。
三阶中心矩和标准差的三次方的比值为偏度,记为 \(\gamma_1 = \mu_3/\sigma^3\)。偏度主要衡量随机变量分布的的不对称性。
\(\gamma_1=0\) 表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布。
\(\gamma_1>0\) 表示概率分布具有右偏性质
\(\gamma_1<0\) 表示概率分布具有左偏性质
四阶中心矩和标准差的四次方的比值为峰度,记为 \(\gamma_2 = \mu_4/\sigma^4\)。峰度可以用来度量随机变量概率分布的陡峭程度。
- 峰度的取值范围为 \([1,+\infty)\),完全服从正态分布的数据的峰度值为 3,峰度值越大,概率分布图越高尖,峰度值越小,越矮胖。
原点矩和中心距之间的关系:
\[\begin{align*} \mu_2 &= \int_{-\infty}^{\infty}(x-\mu)^2f(x)dx\\ &=\int_{-\infty}^{\infty}(x^2-2x\mu+\mu^2) f(x)dx\\ &=\mathbb{E}(X^2)-2\mu\mathbb{E}(X) + \mu^2\\ &=\mu_2'-\mu^2. \end{align*}\]
2.6 概率母函数和矩母函数
随机变量的概率母函数或矩母函数与其分布函数存在一一对应的关系,同样可以描述随机变量的随机特征。
离散型随机变量: 概率母函数 (Probability Generating Function, pgf)
连续性随机变量: 矩母函数 (Moment Generating Function, mgf)
概率母函数或矩母函数可以得到随机变量各阶矩。
【定义】:离散随机变量 \(N\) 的(概率)母函数表示为: \[ P_N(t)=E(t^N)=\sum_{k=0}^{\infty}t^kP(N=k) \]
运用概率母函数可以表示出随机变量 \(N=k\) 的概率,即 \(\Pr(N=k)\) 为概率母函数的 \(k\) 阶偏导在 \(0\) 点出的取值。例如: \[ P(N=1)=\frac{P_N^{(1)}(0)}{1!}\]
\[P(N=k)=\frac{P_N^{(k)}(0)}{k!} \] 其中,\(P_N^{(k)}(\cdot)\) 表示概率母函数的 \(k\) 阶偏导,\(k!=\Gamma(k)\) 表示 \(k\) 阶乘。
【定义】:连续型随机变量 \(X\) 的矩母函数表示为 \[M_X(t)=E(e^{tX})=\int_{-\infty}^{\infty}e^{tX}f(x)dx\]
运用矩母函数可以得到多个独立随机变量之和的分布函数。例如,假设\(S=X_1+X_2+...+X_n=\sum_{i=1}^{n}X_i\),则随机变量 \(S\) 的矩母函数表示为: \[M_s(t)=M_{X_1}(t)M_{X_2}(t)...M_{X_n}(t)\] 其中,\(M_{X_j}(t)\) 表示 \(X_j\) 的矩母函数在 \(t\) 的取值。
2.7 截断和删失
保险中的损失通常指被保险人发生的损失,索赔索赔通常指保险人给被保险人的赔款。由于不同的保险产品通常存在免赔额和赔偿限额的情况,使得保险的损失和索赔的随机性通常是不一致的。
这种不一致性通常运用截断和删失的方法进行处理。
假设随机变量 \(X\) 表示原始的损失,其数学期望可以表示为: \[\mathbb{E}(X)=\int_{0}^{\infty }{S(x)dx}\]
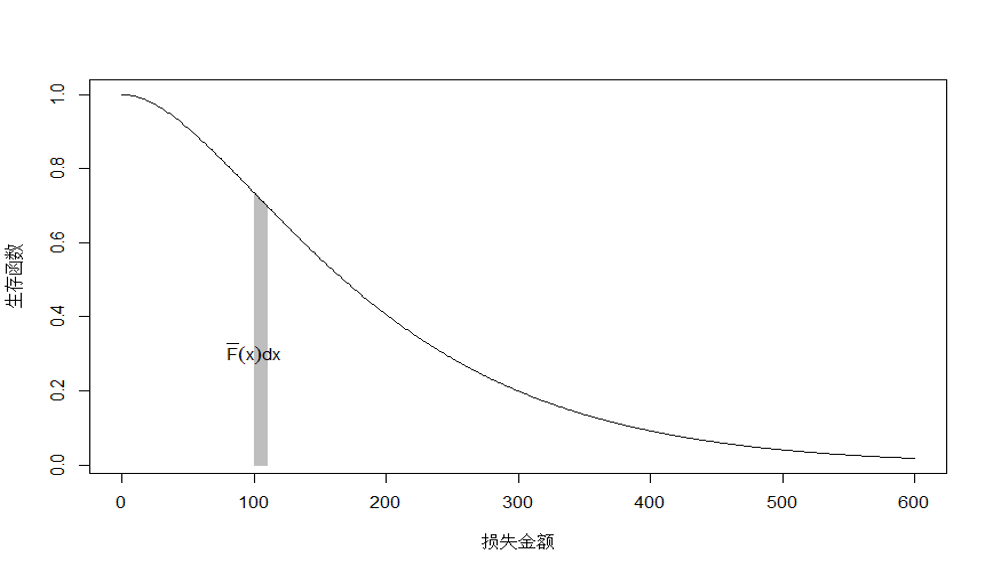
Figure 2.4: 随机变量 \(X\) 的数学期望
2.7.1 左截断(left truncated)和平移(shifted)
【定义】:左截断平移变量定义为: \[ Y^p = X - d|X>d = \begin{cases} \text{NA}, \quad X\le d \\ X - d, \quad X> d \end{cases} \] 其中,\(d\) 为给定常数,且 \(\Pr(X > d) > 0\)。
\(Y^p\) 也称之为 超额损失变量 (excess loss variable)。
\(Y^p\) 是 \(X\) 在 \(d\) 处左截断得到的,原因在于任意 \(X\) 小于 \(d\) 的值都是无法观测到
\(Y^p\) 左截断之后向左平移得到的,因此在截断基础上减少了 \(d\)
随机变量 \(Y^p\) 的数学期望称之为 平均超额损失函数: \[ e_X(d):=\mathbb{E}(Y^p)=\mathbb{E}(X-d|X>d) \]
当 \(X\) 表示保险事故造成的损失金额,\(d\)表示保险免赔额时,则平均超额损失表示已发生的超过免赔额 \(d\) 的期望索赔金额
当 \(X\) 是死亡年龄,平均超额损失表示为已知某人在年龄 \(d\) 存活的情况下的期望预期寿命
平均超额损失函数表示为 \[ {{e}_{X}}(d)=\mathbb{E}\left( X-d|X>d \right)=\frac{\int_{d}^{\infty }{{S}(x)dx}}{S(d)}. \]
【证明】:
\[\begin{align*} {{e}_{X}}(d)&=\frac{\int_{d}^{\infty }{(x-d)f(x)dx}}{1-F(d)}\\ &=\frac{-(x-d)S(x)|_{d}^{\infty }+\int_{d}^{\infty }{S(x)dx}}{S(d)}\\ &=\frac{\int_{d}^{\infty }{S(x)dx}}{S(d)}. \end{align*}\]
下面证明 \((x-d)S(x)|_{d}^{\infty }=0\)
\[\begin{align*} & \underset{x\to \infty }{\mathop{\lim }}\,xS(x)=\underset{x\to \infty }{\mathop{\lim }}\,x\int\limits_{x}^{\infty }{f(t)dt} \\ & =\underset{x\to \infty }{\mathop{\lim }}\,\int\limits_{x}^{\infty }{xf(t)dt} \\ & \le \underset{x\to \infty }{\mathop{\lim }}\,\int\limits_{x}^{\infty }{tf(t)dt} \\ & =\underset{x\to \infty }{\mathop{\lim }}\,\left[ \int\limits_{0}^{\infty }{tf(t)dt}-\int\limits_{0}^{x}{tf(t)dt} \right]=0 \end{align*}\]
2.7.2 左删失(left censored)和平移(shifted)
【定义】:左删失平移 变量定义为: \[ {{Y}^{L}}={{\left( X-d \right)}_{+}}= \begin{cases} & 0,\quad \quad \quad X\le d \\ & X-d,\quad X>d \\ \end{cases} \]
左删失表示随机变量 \(X<d\) 的取值都替换为 \(d\)
平移表示将左删失的变量向左进行平移变化,使得左删失变量减去 \(d\)
\({Y}^{L}\) 的期望表示为: \[ \mathbb{E}[(X-d)_{+}]={\int_{d}^{\infty}(x-d)f(x)dx}=\int_{d}^{\infty}S(x)dx \]
假设 \(X\) 表示损失,则 \(Y^L\) 和 \(Y^P\) 都表示赔款。两者的含义不同:
\(Y^L\) 是含零赔款(per loss),即当保险事故造成的损失没有产生赔款的时候, \(Y^L=0\)
\(Y^P\) 是非零赔款(per payment),即当保险事故造成的损失没有产生赔款的时候, \(\Pr(Y^p=0)=0\)
数学期望存在下述关系:
\[\mathbb{E}[Y^L]=\mathbb{E}[Y^p][1-F_X(d)]\]
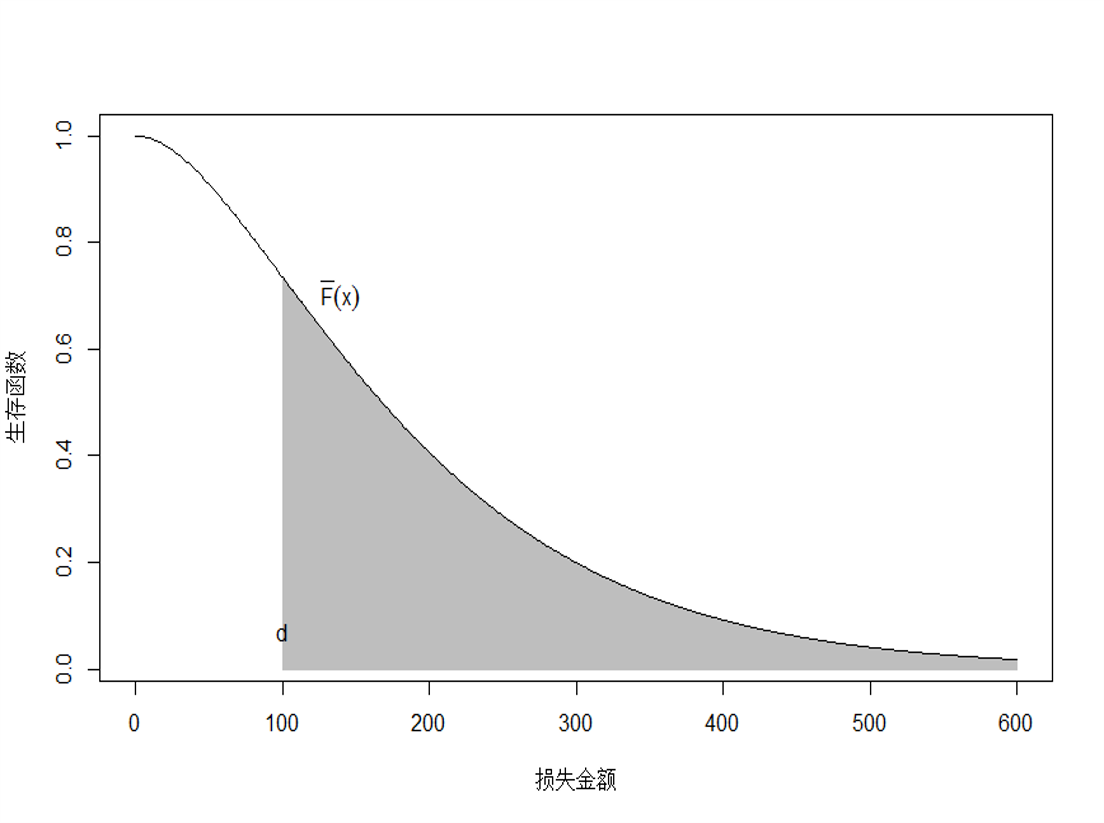
Figure 2.5: 随机变量 \(Y^L\) 的数学期望
2.7.3 右删失(right censored)
【定义】:右删失变量表示为: \[ Y=X\wedge u=\min (X,u)=\begin{cases} & X,\ \ \ X<u \\ & u,\ \ \ \ X\ge u \\ \end{cases} \] 其中,\(Y\) 也被称之为有限损失 (limited loss variable)。
右删失表示随机变量 \(X>u\) 的所有取值都用 \(u\) 代替
\(Y\) 的数学期望 \(E(X\wedge u)\) 称之为有限期望 (limited expected value),表示为:
\[\begin{align*} E(X\wedge u)& =\int_{0}^{u}{xf(x)dx}+u\cdot S(u) \\ & =-xS(x)\left| _{0}^{u} \right.+\int_{0}^{u}{S(x)dx}+uS(u) \\ & =\int_{0}^{u}{S(x)dx} \end{align*}\]
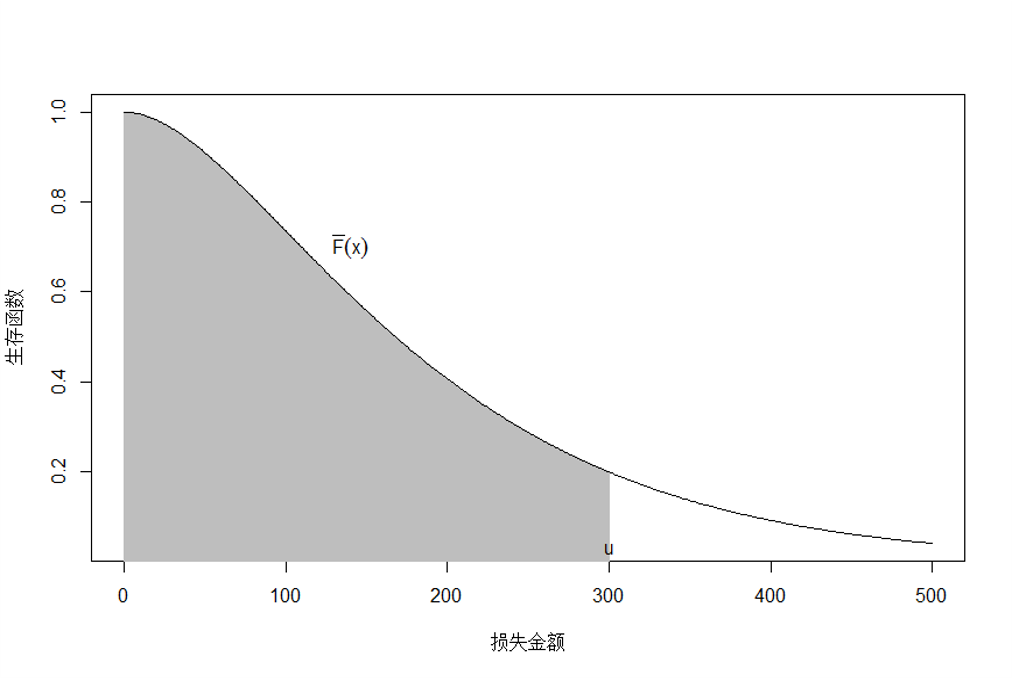
Figure 2.6: 右删失变量的数学期望
2.8 课后习题
1、假设随机变量 \(X\) 的密度函数如下:
\[ f_{X}(x)=\frac{1}{\theta}\exp\left(-\frac{1}{\theta}x\right), x>0, \] 其中,随机变量的期望 \(\mathbb{E}(X)=\theta=200\)。
请用 R 软件进行绘图:
请画出 \(\mathbb{E}(Y^L)\) 和 \(\mathbb{E}(Y^p)\) 随着 \(d\) 增加而变化的曲线图
请画出有限期望 \(\mathbb{E}(X\wedge u)\) 随着 \(u\) 变化而变化的曲线图
# 随机变量 X 分布的生存函数可以表示为
S <- function(x) exp(-200*x)
# 平均超额函数 ex1
ex1 <- NULL
d1 <- seq(0.1, 2, 0.1)
# 运用 integrate 计算函数的积分
for(i in 1:length(d1)){
ex1[i] <- integrate(S, d1[i], Inf)$value/S(d1[i])
}
# 绘图
plot(d1, ex1, type = 'l', ylab = 'mean excess function', ylim = c(0,0.01))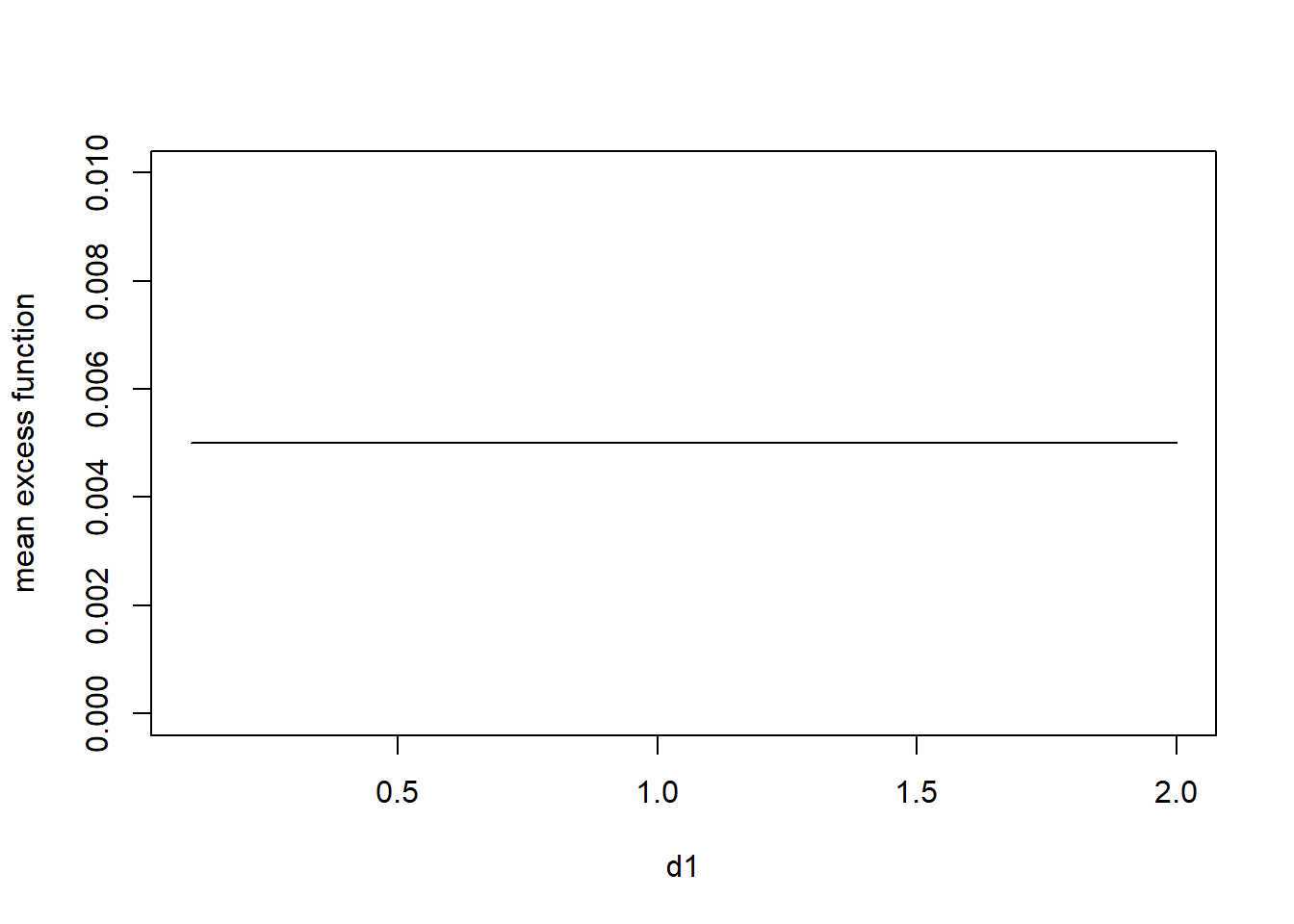
2、假设损失金额服从下述概率分布:
\[ f(x)=\frac{4(100-x)^3}{100^4},\quad\quad 0<x\le 100. \]
- 请计算含零赔款的期望值 \(\mathbb{E}(X \wedge 60)\)。
3、损失随机变量 \(X\) 的分布函数如下:
| \(x\) | \(F(x)\) | \(\mathbb{E}(X\wedge x)\) |
|---|---|---|
| 0 | 0.0 | 0 |
| 100 | 0.2 | 91 |
| 200 | 0.6 | 153 |
| 1000 | 1.0 | 331 |
- 请计算含有 \(d = 100\) 的平均超额损失。