Chapter 3 基本的损失分布
学习目标:
掌握基本的损失金额分布
掌握函数变换生成新分布的方法
掌握基本的损失次数分布,理解 (a, b, 0) 和 (a, b, 1) 的区别,能够计算对应的概率值
能够运用 R 语言调用或者定义损失次数和损失金额分布
3.1 损失金额分布
对保险损失金额进行分析和预测,是精算师和风险管理者的重要工作。通常情况下,保险损失金额具有不对称、定义域非负、尾部较厚的特点,像正态分布等高斯类的分布不适于拟合损失金额。这一节将主要介绍几种常见的损失分布(偏态),以及分布函数、概率密度函数、矩母函数等分布性质。主要包括:
指数分布 (Exponential)
伽马分布(Gamma)
威布尔分布(Weibull)
帕累托分布(Pareto)
对数正态分布(Log-normal)
3.1.1 指数分布 (Exponential)
指数分布通常有两种参数化的形式。
第一种参数化的概率密度函数和累积分布函数为: \[ \begin{aligned} f(x;\theta)&=\frac{1}{\theta}\exp\left({-\frac{1}{\theta}x}\right),\quad x > 0,\\ F(x;\theta)&=1-\exp\left({-\frac{1}{\theta}x}\right). \end{aligned} \]
第二种参数化的概率密度函数和累积分布函数为: \[ \begin{aligned} f(x;\lambda)&=\lambda\exp\left({-\lambda x}\right),\quad x > 0,\\ F(x;\lambda)&=1-\exp\left({-\lambda x}\right), \end{aligned} \] 其中,\(\lambda=\frac{1}{\theta}\) 为比率参数。
指数分布的期望、方差分别为 \[\mathbb{E}(X)=\theta,\] \[\text{Var}(X)=\theta^2.\]
指数分布具有无记忆性,即 \[\Pr(X>x+u|X>u)=\Pr(X>x).\]
指数分布的缺点是其概率密度函数是单调递减的,这在很多情况下,并不适于实际的需要。
# ==========================================
# 指数分布
# ===========================================
theta <- c(0.5, 1, 2)
x0 <- seq(0.001, 10, length.out = 100)
par(mfrow = c(1, 1) )
f1 <- dexp(x0, rate = 1/theta[1], log = FALSE)
f2 <- dexp(x0, rate = 1/theta[2], log = FALSE)
f3 <- dexp(x0, rate = 1/theta[3], log = FALSE)
matplot(x0, cbind(f1, f2, f3), type = 'l', lty = 1:3, lwd = 2)
legend('topright',
legend = c('theta = 0.5', 'theta = 1', 'theta = 2'),
lty = c(1,2,3),
bty = "n", lwd = 2, col = 1:3)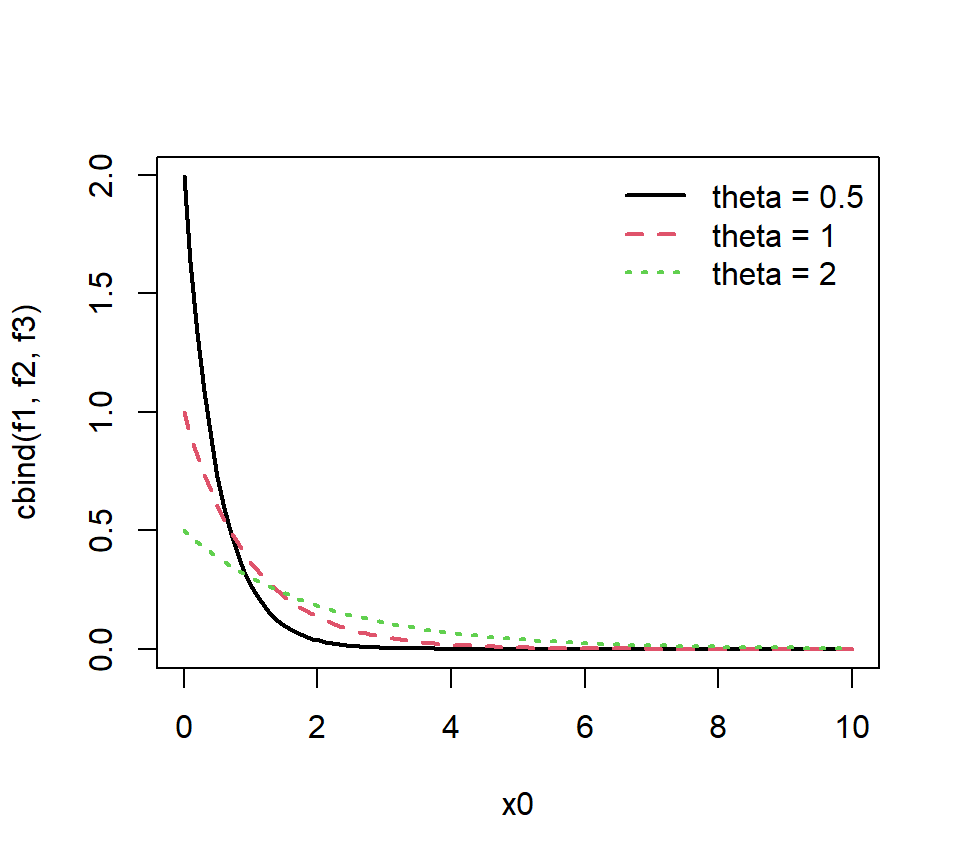
Figure 3.1: 指数分布的密度函数图
3.1.2 伽马分布(Gamma)
第一种伽马分布的概率密度函数为 \[ f(x; \alpha, \theta)=\frac{{{\theta }^{-\alpha }}}{\Gamma \text{(}\alpha )}{{x}^{\alpha -1}}{{e}^{-\frac{1}{\theta} x}}.\]
其中 \(\alpha\) 是 形状参数,\(\theta\) 是 尺度参数。
伽马分布的期望、方差分别为 \[\mathbb{E}(X)=\alpha/\beta\] \[\text{Var}(X)=\alpha/\beta^2.\]
第二种伽马分布的概率密度函数为: \[ f(x; \alpha, \beta)=\frac{{{\theta }^{\alpha }}}{\Gamma \text{(}\alpha )}{{x}^{\alpha -1}}{{e}^{-\beta x}}.\]
其中 \(\alpha\) 是 形状参数,\(\beta=1/\theta\) 是 比率参数。
第三种伽马分布的概率密度函数为: \[ f(x;\mu, \phi)=\frac{{{(\phi\mu)}^{-1/\phi }}}{\Gamma \text{(}1/\phi )}{{x}^{1/\phi -1}}{{e}^{-\frac{1}{\phi\mu} x}}, \] 其中,\(\mu=\alpha/\beta\) 是均值参数,\(\phi=1/\alpha\) 是离散参数。均值和方差分别为 \(\mu\) 和 \(\phi\mu^2\)。
【定理】 伽马分布具有可加性:假设两个随机变量 \(X_1\) 和 \(X_2\) 都服从形状参数\(\alpha_1\)和\(\alpha_2\) ,比率参数都为 \(\beta\) 的伽马分布,即 \(X_1\sim GA(\alpha_1,\beta)\),\(X_2\sim GA(\alpha_2,\beta)\) ,那么随机变量之和\(X_1+X_2\) 服从形状参数为 \(\alpha_1+\alpha_2\),比率参数为\(\beta\) 的伽马分布,即\[X_1+X_2\sim GA(\alpha_1+\alpha_2,\beta).\]
当形状参数\(\alpha=1\)时,伽马分布可以退化为指数分布,即指数分布是伽马分布的特例。
当\(\alpha=n/2\)和\(\beta=1/2\) 时,伽马分布可以退化为卡方分布,其中卡方分布的自由度为\(n/2\)。
# ==========================================
# 伽马分布
# ===========================================
par(mfrow = c(1, 2) )
# 固定形状参数
alpha <- 2 # 形状参数
theta <- c(0.5, 1, 2) # 比率参数,尺度参数为 1/theta
x0 <- seq(0.001, 15, length.out = 100)
f1 <- dgamma(x0, shape = alpha, rate = theta[1]) #
f2 <- dgamma(x0, shape = alpha, rate = theta[2])
f3 <- dgamma(x0, shape = alpha, rate = theta[3])
matplot(x0, cbind(f1, f2, f3),ylim = c(0,0.8), main = '', type = 'l', lty = 1:3, lwd = 2, ylab = '密度函数')
legend('topright', legend = c('alpha = 2, theta = 0.5',
'alpha = 2, theta = 1',
'alpha = 2, theta = 2'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)
# 固定比率参数
alpha <- c(1,2,3)
theta <- 0.5
x0 <- seq(0.001, 15, length.out = 100)
f1 <- dgamma(x0, shape = alpha[1], rate = theta)
f2 <- dgamma(x0, shape = alpha[2], rate = theta)
f3 <- dgamma(x0, shape = alpha[3], rate = theta)
matplot(x0, cbind(f1, f2, f3),ylim = c(0,0.8), main = '', type = 'l', lty = 1:3, lwd = 2, ylab = '密度函数')
legend('topright',legend = c('alpha = 1, theta = 0.5',
'alpha = 2, theta = 0.5',
'alpha = 3, theta = 0.5'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)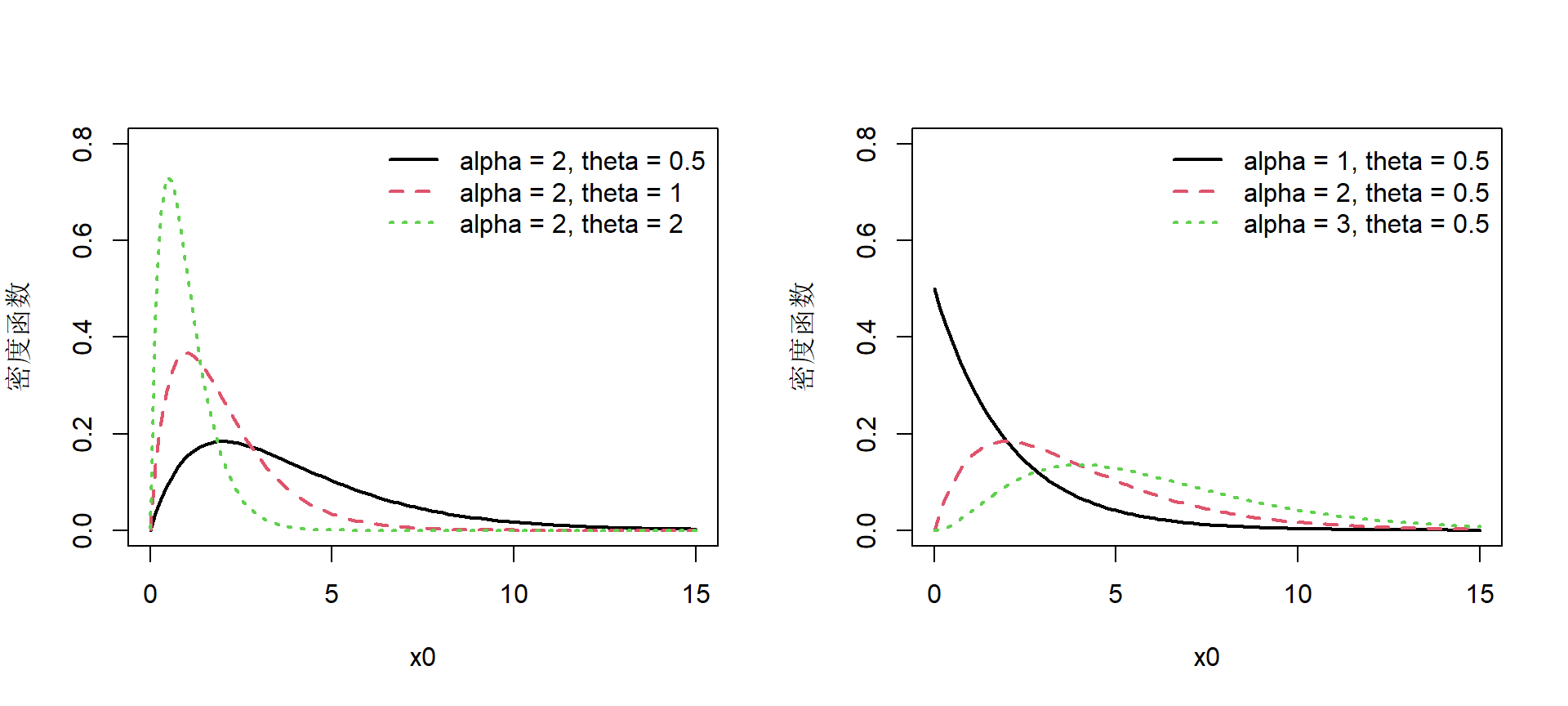
Figure 3.2: 伽马分布密度函数图
3.1.3 帕累托分布(Pareto)
帕累托分布一般分为双参数和单参数两种。若没有特殊说米,一般指双参数帕累托。帕累托分布的分布函数、密度函数、期望和方差分别表示为: \[ \begin{align*} & {{F}_{X}}(x)=1-{{\left( \frac{\theta }{x+\theta } \right)}^{\alpha }}\ \ \ \ 0<x<\infty \\ & \\ & {{f}_{X}}(x)=\frac{\alpha {{\theta }^{\alpha }}}{{{(x+\theta )}^{\alpha +1}}} \\ & \\ & \mathbb{E}(X)=\frac{\theta }{\alpha -1},\ \ \ \ \ \ \text{Var}(X)=\frac{\alpha {{\theta }^{2}}}{{{(\alpha -1)}^{2}}(\alpha -2)}. \end{align*} \]
library(actuar)
# shape = alpha, scale = theta
# mean = 50
alpha <- c(0.5,2,5)
theta <- c(5,50,200)
x0 <- seq(0.001, 100, length.out = 100)
f1 <- dpareto(x0, shape = alpha[1], scale = theta[1])
f2 <- dpareto(x0, shape = alpha[2], scale = theta[2])
f3 <- dpareto(x0, shape = alpha[3], scale = theta[3])
matplot(x0, cbind(f1, f2, f3), main = '', type = 'l',
lty = 1:3, lwd = 2, ylab = 'pdf', ylim = c(0,0.05))
legend('topright', legend = c('alpha = 0.5, theta = 5',
'alpha = 2, theta = 50',
'alpha = 5, theta = 200'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)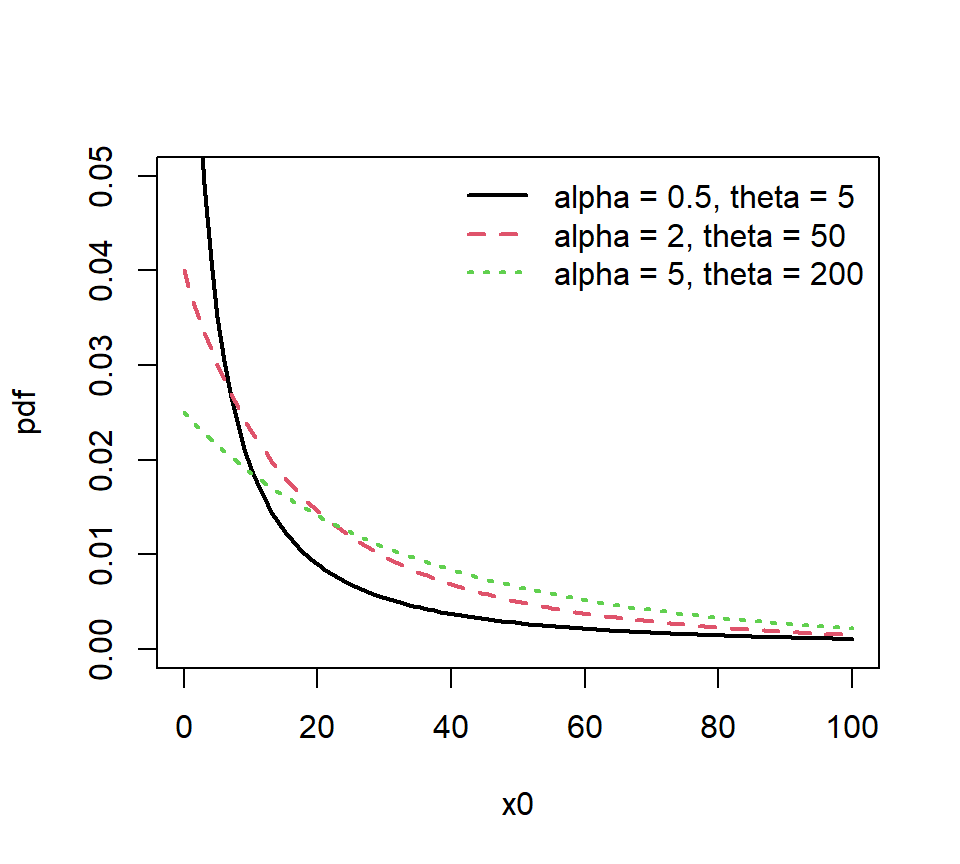
Figure 3.3: 帕累托密度函数图
单参数帕累托的概率密度函数为: \[ \begin{align*} f(x)&=\frac{\alpha\theta^\alpha}{x^{\alpha+1}},\quad x>\theta,\\ F(x)&=1-\left(\frac{\theta}{x}\right)^\alpha, \end{align*} \]
其中 \(\alpha\) 是真实参数,\(\theta\) 是预先给定的。
单参数帕累托的 \(k\) 阶矩为:
\[ \mathbb{E}(X^k)=\frac{\alpha \theta^k}{\alpha-k},\quad k < \alpha. \]
library(actuar)
# shape = alpha, scale = theta
# mean = 50
alpha <- c(0.5,2,5)
theta <- c(20,50,80)
x0 <- seq(0.001, 200, length.out = 100)
f1 <- dpareto1(x0, shape = alpha[1], min = theta[1])
f2 <- dpareto1(x0, shape = alpha[2], min = theta[2])
f3 <- dpareto1(x0, shape = alpha[3], min = theta[3])
matplot(x0, cbind(f1, f2, f3), main = '', type = 'l',
lty = 1:3, lwd = 2, ylab = 'pdf', ylim = c(0,0.08))
legend('topright', legend = c('alpha = 0.5, theta = 5',
'alpha = 2, theta = 50',
'alpha = 5, theta = 200'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)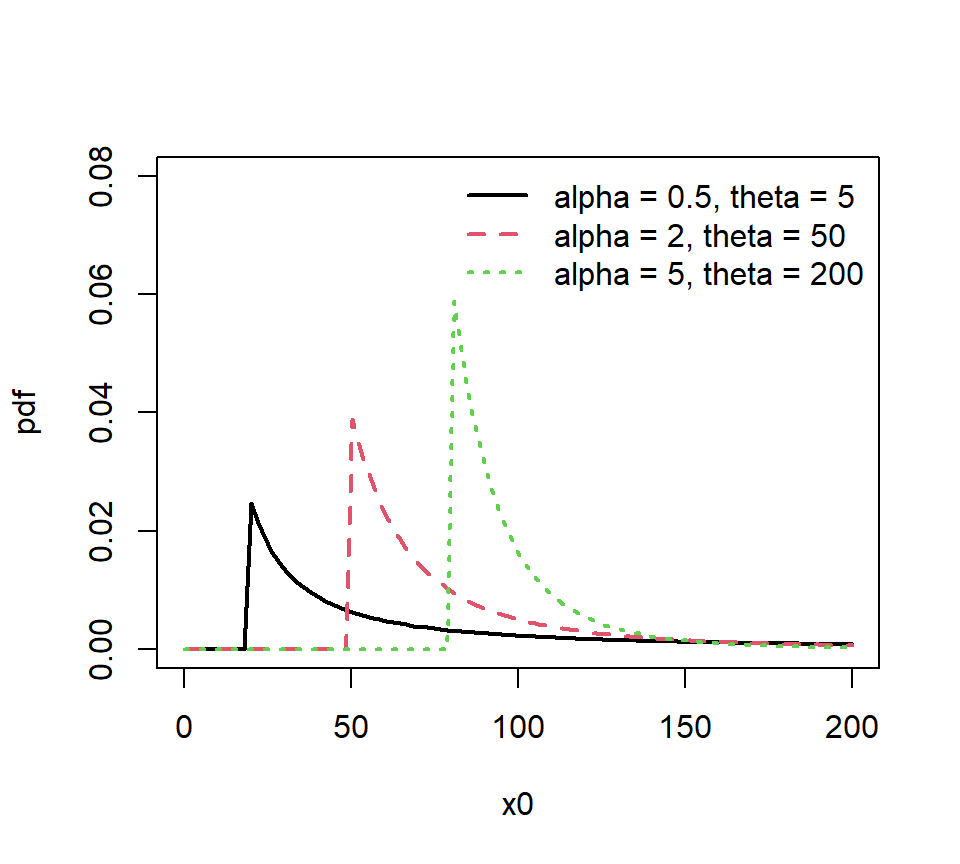
Figure 3.4: 单参数帕累托密度函数图
3.1.4 对数正态分布(Log-normal)
对数正态分布的概率密度函数和分布函数为 \[ f(x)=\frac{1}{x\sigma}\phi\left(\frac{\ln x - \mu}{\sigma} \right) =\frac{1}{x\sigma\sqrt{2\pi}}\exp\left[ -\frac{1}{2}\left(\frac{\ln x - \mu}{\sigma} \right)^2 \right] \]
对数正态分布的均值和方差分别为
\[ \mathbb{E}(X)=\exp\left(\mu + \frac{1}{2}\sigma^2\right) \] \[ \text{Var}(X)=(e^{\sigma^2}-1)e^{2\mu+\sigma^2} \]
假设随机变量服从参数为\((\mu,\sigma)\)的正态分布\(X\sim N(\mu,\sigma^2)\) ,那么随机变量\(Y=e^X\)则服从参数为\((\mu,\sigma)\) 的对数正态分布。
对数正态分布的参数\(\mu\)和\(\sigma\) 并不是它的均值和方差。
对数正态分布的概率密度函数是右偏、厚尾的,因而可以很好地拟合许多损失分布的情形。
当\(\sigma\)很小的时候,对数正态分布与正态分布非常相似。
# ===========================================
# 对数正态分布
# ===========================================
par(mfrow = c(1, 2) )
# 固定 mu
mu <- 2
sigma <- c(0.5, 1, 2)
x0 <- seq(0.001, 15, length.out = 100)
f1 <- dlnorm(x0, meanlog = mu, sdlog = sigma[1])
f2 <- dlnorm(x0, meanlog = mu, sdlog = sigma[2])
f3 <- dlnorm(x0, meanlog = mu, sdlog = sigma[3])
matplot(x0, cbind(f1, f2, f3), main = '', type = 'l', lty = 1:3, lwd = 2, ylab = '密度函数')
legend('topright',legend = c('mu = 2, sigma = 0.5',
'mu = 2, sigma = 1',
'mu = 2, sigma = 2'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)
# 固定 sigma
mu <- c(1,2,3)
sigma <- 1
x0 <- seq(0.001, 15, length.out = 100)
f1 <- dlnorm(x0, meanlog = mu[1], sdlog = sigma)
f2 <- dlnorm(x0, meanlog = mu[2], sdlog = sigma)
f3 <- dlnorm(x0, meanlog = mu[3], sdlog = sigma)
matplot(x0, cbind(f1, f2, f3), main = '', type = 'l', lty = 1:3, lwd = 2, ylab = '密度函数')
legend('topright', legend = c('mu = 1, sigma = 1',
'mu = 2, sigma = 1',
'mu = 3, sigma = 1'),
lty = c(1,2,3), bty = "n", lwd = 2, col = 1:3)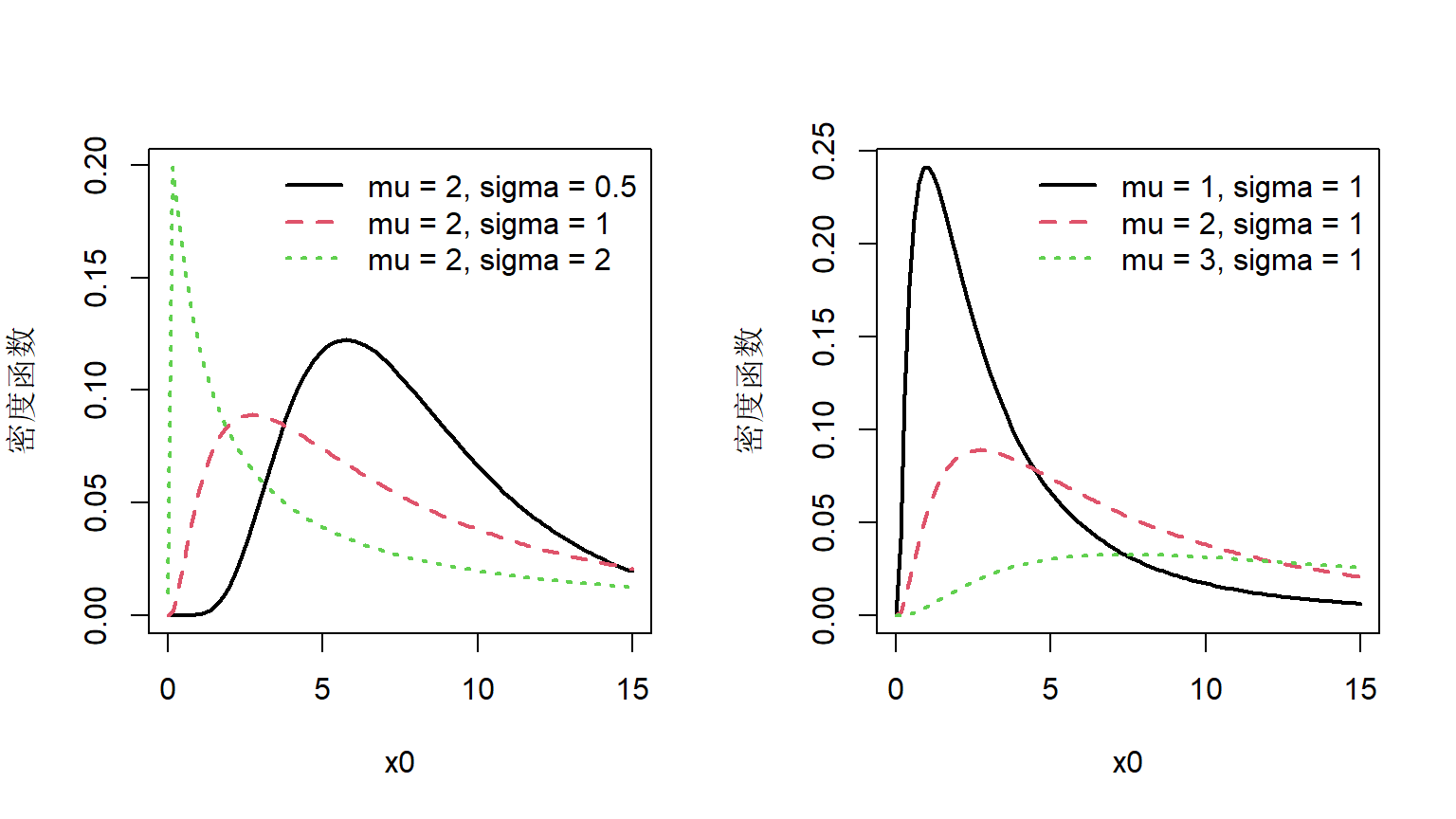
Figure 3.5: 对数正态密度函数图
3.2 损失次数分布
在非寿险精算中,通常用用计数随机变量来描述一段时间内发生的损失次数或索赔次数。计数随机变量是离散型随机变量的一种,随机变量的取值是在 \(0,1,2, 3,4...\) 正整数值域。常见的损失次数包括:泊松分布、负二项分布和二项分布。
3.2.1 泊松分布(Poisson)
泊松分布的概率密度函数: \[ {{p}_{k}}=\frac{{{e}^{-\lambda }}{{\lambda }^{k}}}{k!},\quad k=0,1,2.... \] 概率母函数: \[ P(z)=e^{(\lambda(z-1))},\quad \lambda>0. \] 均值和方差可以通过母函数求得: \[ \begin{align*} \mathbb{E}(N)&=\lambda \\ \text{Var}(N)&=\lambda \end{align*} \]
泊松分布的方差和均值相等,都可以表示为\(\lambda\)。
若干个独立的泊松分布之和仍然服从泊松分布。
泊松分布可以分解为若干个泊松分布之和。
# density function 概率函数
#dpois(x, lambda, log = FALSE) # lambda 表示均值, log = TRUE 表示输出log(f(x))
# distribution function 分布函数
#ppois(q, lambda, lower.tail = TRUE, log.p = FALSE)
# quantile function 分布函数的逆函数(分位数函数)
#qpois(p, lambda, lower.tail = TRUE, log.p = FALSE)
# 泊松分布的随机数 - 模拟
#rpois(n, lambda = 10) # 模拟 n 个服从期望为10的泊松分布
# 画图- 不同lambda的泊松分布的概率函数图
par(mfrow = c(2,2))
lambda.po <- c(1, 2, 5, 10) # lambda 取值为 1,2,5,10
x0 <- seq(0, 20) # x 取值为 0-25 的整数
for(lambda.po in c(1, 2, 5, 10)){
barplot(dpois(x0, lambda.po), names.arg = x0, main = paste('lambda = ', lambda.po, sep = ''))
}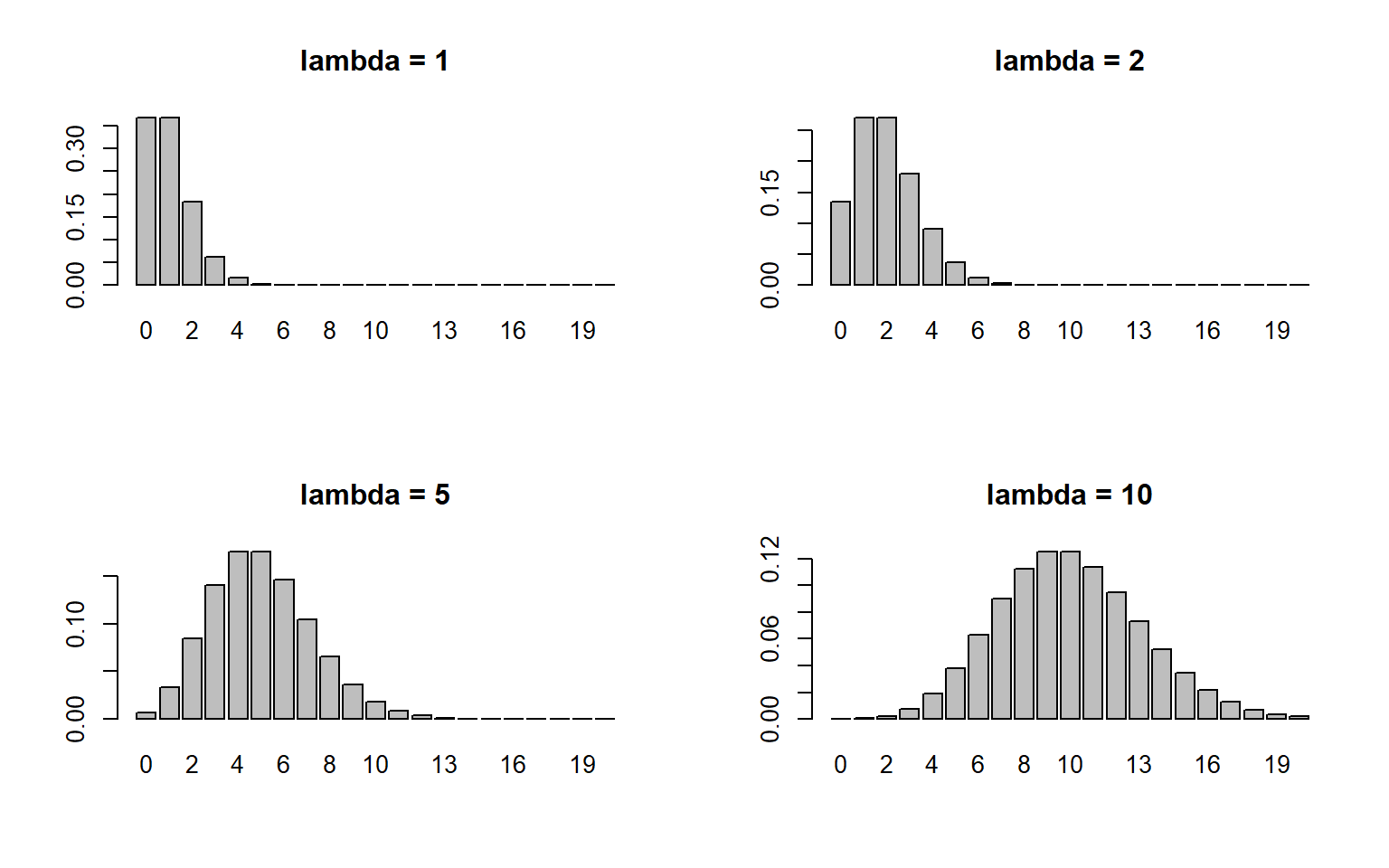
Figure 3.6: 泊松分布的概率函数图
【例】: 假设索赔次数 \(N\) 服从参数为 的泊松分布,请计算:
索赔次数等于 3 的概率 \(\Pr(N=3)\)
索赔次数小于等于 4 的概率 \(\Pr(N\leq4)\)
索赔次数大于等于 3 小于等于 5 的概率 \(\Pr(3\leq N \leq 5)\)
## 索赔次数等于3的概率
dpois(3, lambda = 2)## [1] 0.180447## 索赔次数小于等于4的概率为
ppois(4, lambda = 2)## [1] 0.947347## 索赔次数大于等于3小于等于5的概率
ppois(5, 2) - ppois(2, 2)## [1] 0.306763.2.2 负二项分布(Negative Binomial distribution)
负二项分布的概率密度函数: \[ {{p}_{k}}=\frac{\Gamma (k+r)}{\Gamma (r)\Gamma (k+1)}{{\left( \frac{1}{1+\beta } \right)}^{r}}{{\left( \frac{\beta }{1+\beta } \right)}^{k}}, \quad k=0,1,2,.... \]
负二项分布的概率母函数表示为
\[ P(z)={{\left[ 1-\beta (z-1) \right]}^{-r}} \]
期望和方差分别表示为:
\[ \begin{align*} \mathbb{E}(X)&=r\beta\\ \text{Var}(X)&=r\beta(1+\beta) \end{align*} \] 【证明】:
\[ \begin{align*} P(z)&=\sum\limits_{k=0}^{\infty }{{{p}_{k}}{{z}^{k}}}\\ &=\sum\limits_{k=0}^{\infty }{\left[ \frac{\Gamma (k+r)}{\Gamma (r)\Gamma (k+1)}{{\left( \frac{1}{1+\beta } \right)}^{r}}{{\left( \frac{\beta }{1+\beta } \right)}^{k}} \right]{{z}^{k}}} \\ & =\sum\limits_{k=0}^{\infty }{\left[ \frac{\Gamma (k+r)}{\Gamma (r)\Gamma (k+1)}{{\left( \frac{1+\beta -z\beta }{1+\beta } \right)}^{r}}{{\left( \frac{z\beta }{1+\beta } \right)}^{k}} \right]}{{\left( 1+\beta -z\beta \right)}^{-r}} \\ & ={{\left( 1+\beta -z\beta \right)}^{-r}} \end{align*} \]
注意:几何分布是负二项分布在\(r=1\)时的特殊情况。
令 \(p=\frac{1}{1+\beta}\), 负二项分布密度函数的另一种形式: \[ {{p}_{k}}=\frac{\Gamma (k+r)}{\Gamma (r)\Gamma (k+1)}{{p}^{r}}{{\left( 1-p \right)}^{k}} \]
其中,负二项分布的方差大于均值,通常可以用来描述具有过离散数据特征的损失次数。
下图显示了参数 \(r\) 在不同取值条件下负二项分布的概率分布图。可以发现,当负二项分布均值越大时,分布形状约趋近于正态分布。
# 负二项分布的概率函数
r0 <- c(1, 1, 2, 2)
p0 <- c(0.3,0.5, 0.3, 0.5)
x0 <- seq(0, 20)
ylim0 <- list(c(0,0.5),
c(0,0.5),
c(0,0.5),
c(0,0.5)) # 上下界
par(mfrow = c(2, 2) )
for (i in 1:length(p0)){
fpo <- dnbinom(x0, size = r0[i], prob = p0[i], log = FALSE)
barplot(fpo,
main = paste0('r = ', r0[i], ', ','p = ', p0[i]),
names.arg = x0, ylim = ylim0[[i]]
)
}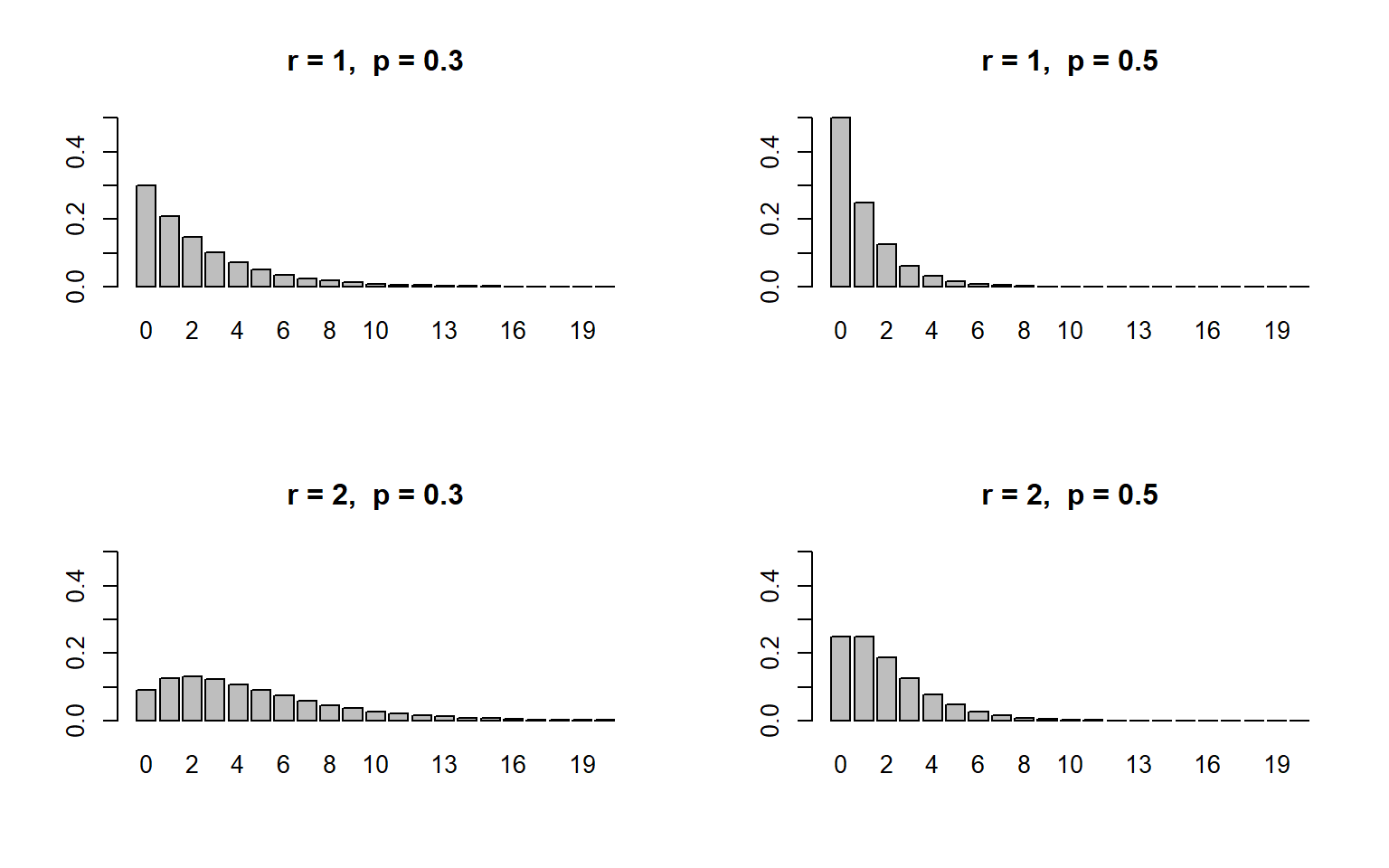
Figure 3.7: 负二项分布的概率函数图
- 令 \(r\to\infty\) 且 \(\beta\to 0\),令 \(r\beta=\lambda\) 是一个常数,可以发现 \[ \begin{align*} \mathbb{E}(X)&=r\beta \to \lambda\\ \text{Var}(X)&=r\beta(1+\beta) \to \lambda \end{align*} \] 负二项分布的极限分布是泊松分布。
3.2.3 二项分布(Binomial Distribution)
个体风险发生索赔的概率为 \(q\), 不发生索赔的概率为 \(1-q\), 则索赔次数分布的母函数为 \[ P\left( z \right)=\mathbb{E}\left( {{z}^{N}} \right)=\left( 1-q \right){{z}^{0}}+q{{z}^{1}}=1-q+qz=1+q\left( z-1 \right) \] 对 \(m\) 个独立同分布的个体风险,其索赔次数分布的母函数为 \[ P\left( z \right)=[1+q\left( z-1 \right)]^m. \] 这 \(m\) 个风险发生\(k\)次索赔的概率为二项分布 \[ {{p}_{k}}=\left(^m _k \right){{q}^{k}}{{(1-q)}^{m-k}}\quad \quad k=0,1,2,...,m. \]
- 二项分布的均值和方差为
\[ \begin{aligned} \mathbb{E}(X)&=mq, \\ \text{Var}(X)&=mq(1-q) \end{aligned} \]
二项分布的取值存在一个最大值\(m\)
参数 \(m>0\) 使得二项分布的均值大于方差,主要用于描述具有欠离散数据特征的损失次数(精算中并不常用)
下图显示二项分布的均值越大,分布形态越对称。
# =============================================================
# 二项分布
# =============================================================
m0 <- c(1, 5, 10, 10, 10, 10)
q0 <- c(0.3, 0.3, 0.3, 0.1, 0.2, 0.3)
x0 <- seq(0, 10)
par(mfrow = c(2, 3) )
for (i in 1:length(m0)){
fpo <- dbinom(x0, size = m0[i], prob = q0[i], log = FALSE)
barplot(fpo,
main = paste0('m = ', m0[i], ', ',
'q = ', q0[i]),
names.arg = x0)
}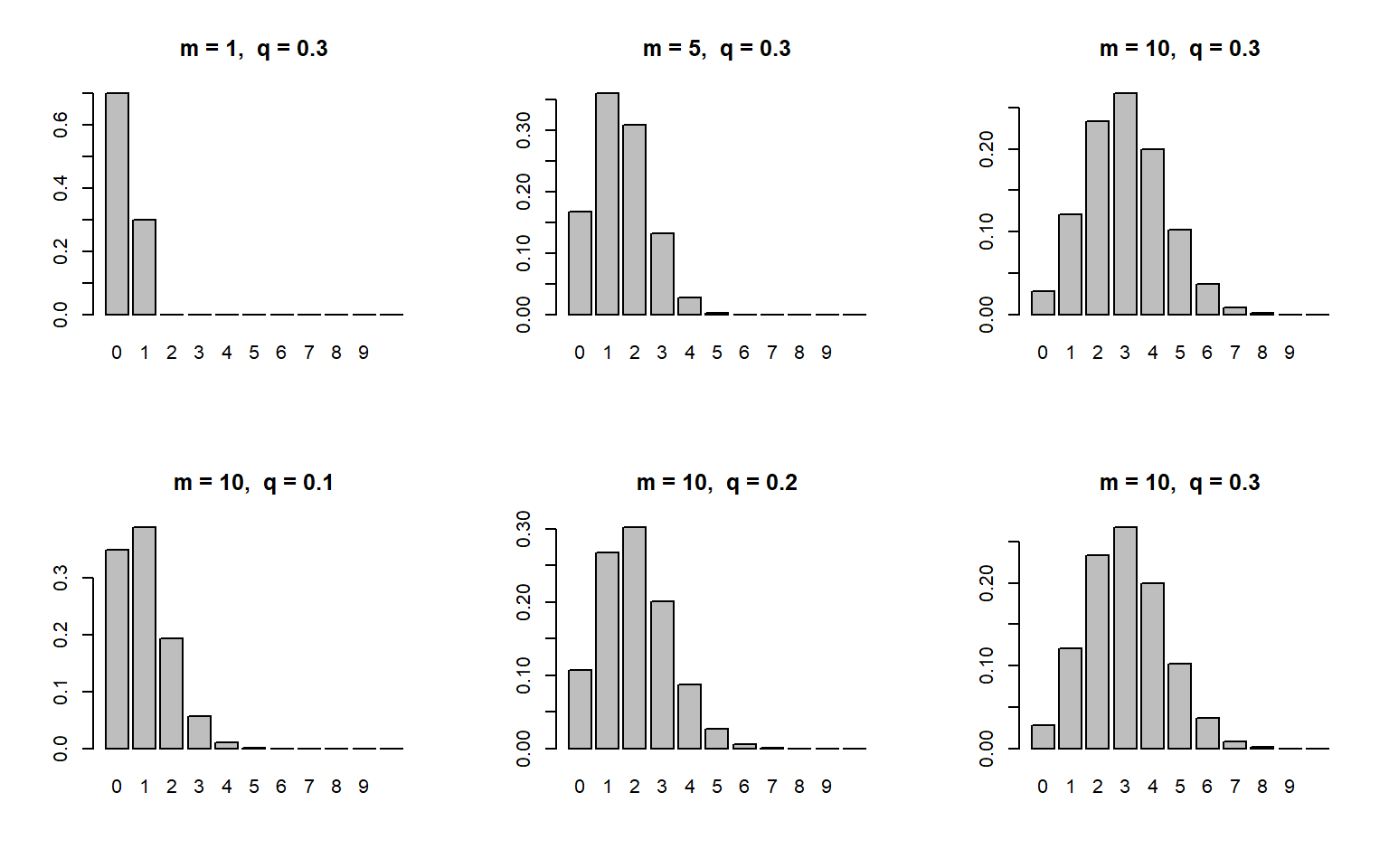
Figure 3.8: 二项分布的概率函数图
3.2.4 \((a,b,0)\) 和 \((a,b,1)\) 分布类
【定义】:\((a,b,0)\) 分布类满足下述递推关系: \[p_k=(a+\frac{b}{k})p_{k-1}, \quad k=1,2,3,...,\] 其中,\(a\) 和 \(b\) 为常数,\(p_k = \Pr(N=k)\)。已知 \(a,b\) 和 \(p_0\),就能唯一确定整个概率分布函数。
\((a,b,0)\) 分布类仅包括:
泊松分布(Poisson)
二项分布(Binomial Distribution)
负二项分布(Negative Binomial distribution)
\((a,b,1)\) 分布类包含两个子类:
零截断分布 (zero-truncated distribution)
零调整分布 (zero-modified distribution)
对于零截断分布,发生 \(k\) 次损失的概率用\(p_k^T\)表示,其中\(p_0^T=0\)
对于零调整分布,发生 \(k\) 次损失的概率用 \(p_k^M\) 表示,其中 \(p_0^M\) 表示可以是任意概率值。
【定义】\((a,b,1)\)分布类满足下述递推关系:
\[p_k=(a+\frac{b}{k})p_{k-1},\quad k=2,3,...\]
递推关系与 \((a,b,0)\) 分布类的递推关系完全相同
\((a,b,1)\) 分布类的递推关系是从 \(p_1\)开始,而\((a,b,1)\)分布类的递推关系是从\(p_0\)开始。
零截断负二项分布的概率计算
## 负二项分布的概率
x = 0:10
p = dnbinom(x,4,0.7)
round(p,3)## [1] 0.240 0.288 0.216 0.130 0.068 0.033 0.015 0.006 0.003 0.001 0.000## 零截断负二项分布的概率
p0 = p[1] ##零点的概率
pt1 = p[2:11]/(1-p0) ##其它点上的概率
pt = c(0, pt1)
round(pt,3)## [1] 0.000 0.379 0.284 0.171 0.090 0.043 0.019 0.008 0.003 0.001 0.001## 绘图比较负二项和零截断负二项的概率
com = rbind(负二项 = p, 零截断负二项 = pt)
barplot(com,beside=TRUE,names.arg=0:10,legend.text=TRUE)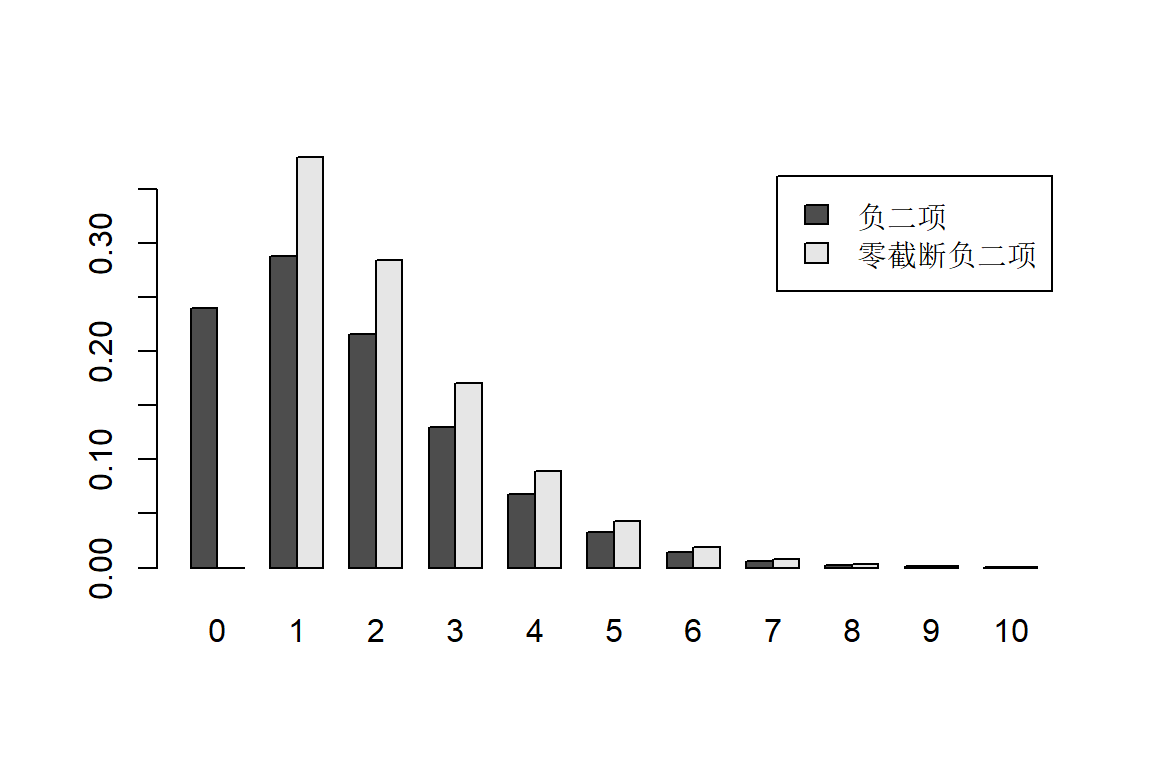
Figure 3.9: 零截断负二项分布的概率函数图
- 零调整负二项分布的计算
## 负二项分布的概率
x = 0:10
p = dnbinom(x, 4, 0.7)
round(p,3)## [1] 0.240 0.288 0.216 0.130 0.068 0.033 0.015 0.006 0.003 0.001 0.000## 零调整负二项分布的概率
p0 = 0.3 ##调整零点的概率
pm = (1-p0)*p[2:11]/(1-p[1]) ##其它点上的概率
pm = c(p0,pm)
round(pm, 3)## [1] 0.300 0.265 0.199 0.119 0.063 0.030 0.014 0.006 0.002 0.001 0.000## 绘图
com = rbind(负二项 = p, 零调整负二项 = pm)
barplot(com, beside = TRUE, names.arg = 0:10,legend.text=TRUE)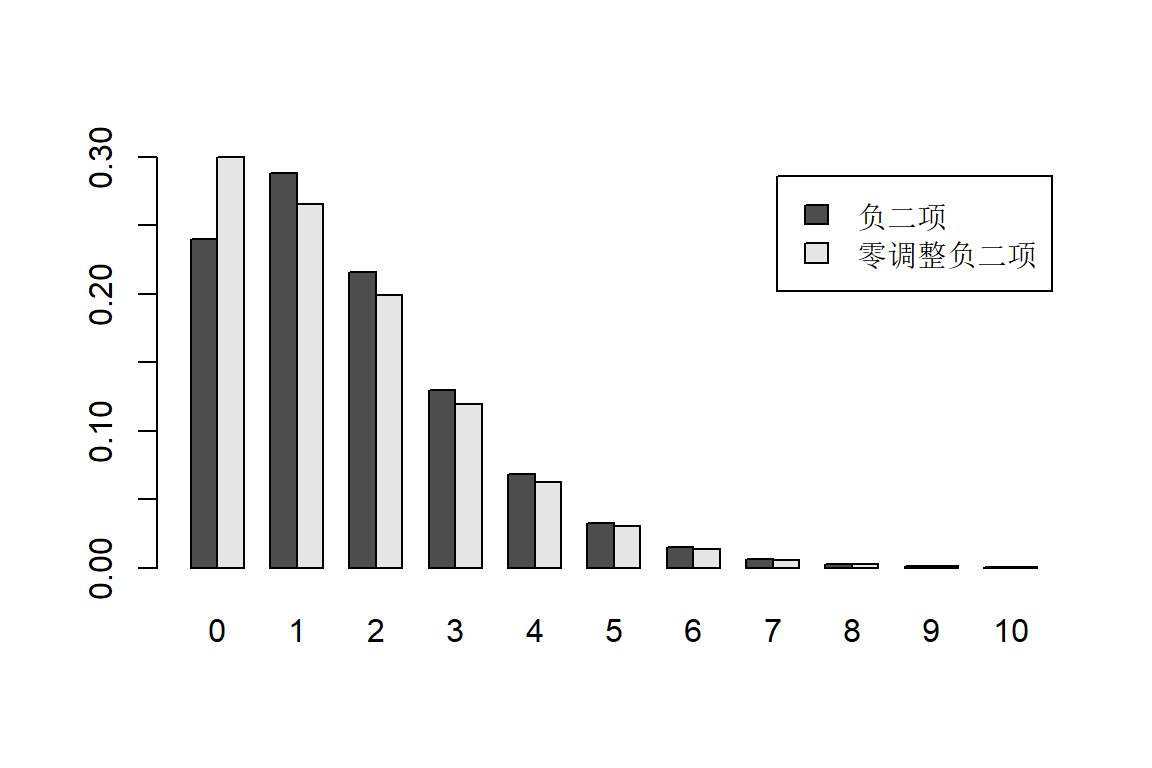
Figure 3.10: 零调整负二项分布的概率函数图
3.3 函数变换生成新分布
通常可以通过函数变换的方法生成新的损失分布。常见的函数变换主要包括:线性变换、幂变换、指数变换和对数变换。
假设随机变量为 \(X\),其分布函数为 \(F_X(\cdot)\),存在调单函数 \(g(\cdot)\),使得随机变量 \(Y=g(X)\)。\(Y\) 的分布函数可以表示为:
\[ \begin{aligned} F_Y(y)&=\Pr(Y\le y) \\ &=\Pr(g(X)\le y)\\ &= \begin{cases} \Pr(X\le g^{-1}(y))=F_X(g^{-1}(y)) \quad \quad \text{若g()为单调递增函数}\\ \Pr(X\ge g^{-1}(y))=F_X(1-g^{-1}(y))\quad \text{若g()为单调递减函数}\\ \end{cases} \end{aligned} \]
随机变量 \(Y\) 的密度函数表示为 \[ f_Y(y)=\frac{dF_Y(y)}{dy} = \begin{cases} \frac{dg^{-1}(y)}{dy} f_X(g^{-1}(y)) \quad \quad \text{若g()为单调递增函数}\\ -\frac{dg^{-1}(y)}{dy} f_X(1-g^{-1}(y))\quad \text{若g()为单调递减函数}\\ \end{cases} \]
【例】:函数变换构造新分布。
假设 \(X\) 服从形状参数为 3, 比率参数为 4 的伽马分布。
求指数变换 \(g(X)\) 的分布。
求对数变换 \(g(X)\) 的分布。
### 伽马分布的密度函数
f = function(x) dgamma(x, shape = 3, rate = 4)
### 指数变换, Y = exp(X)
f1 = function(x) f(log(x))/x
### 对数变换, Y = log(X)
f2 = function(x) f(exp(x)) * exp(x)